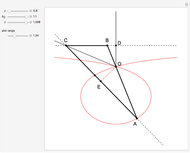
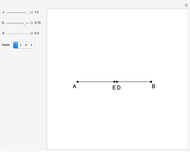
Construction
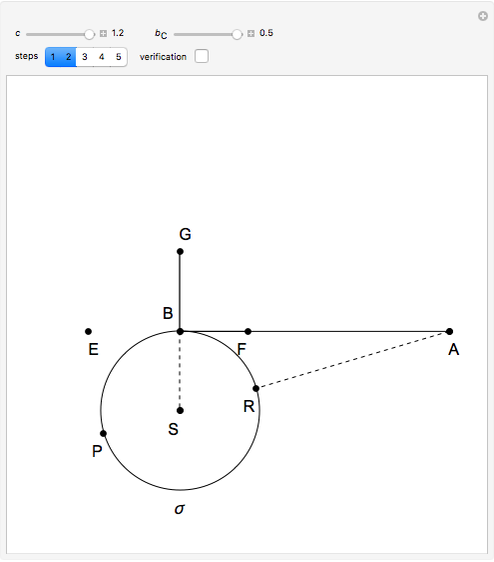
Step 1. Let  have length
have length  .
.
Let the point  be on the perpendicular to
be on the perpendicular to  at
at  such that
such that  . Let
. Let  be the circle with center
be the circle with center  and radius
and radius  .
.
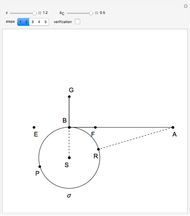
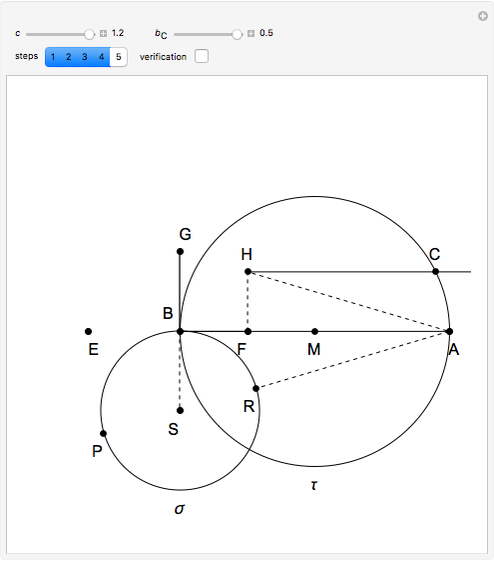
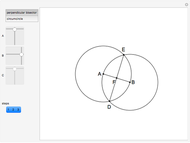
Step 2. Let  and
and  be the intersections of the ray
be the intersections of the ray  and
and  .
.
Let the points  and
and  be on
be on  so that
so that  and
and  . Let
. Let  be the point on the extension of
be the point on the extension of  so that
so that  is the midpoint of
is the midpoint of  .
.
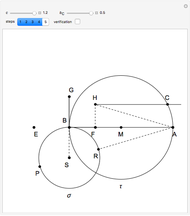
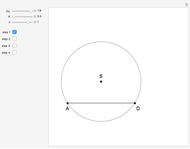
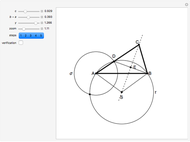
Step 3. Let  be the intersection of the ray
be the intersection of the ray  and the perpendicular to
and the perpendicular to  at
at  .
.
Step 4. Let  be the midpoint of
be the midpoint of  . Let
. Let  be the circle with center
be the circle with center  and radius
and radius  . Let
. Let  be the intersection of
be the intersection of  and the parallel to
and the parallel to  through
through  .
.
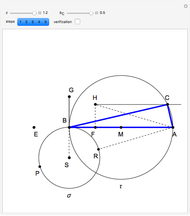
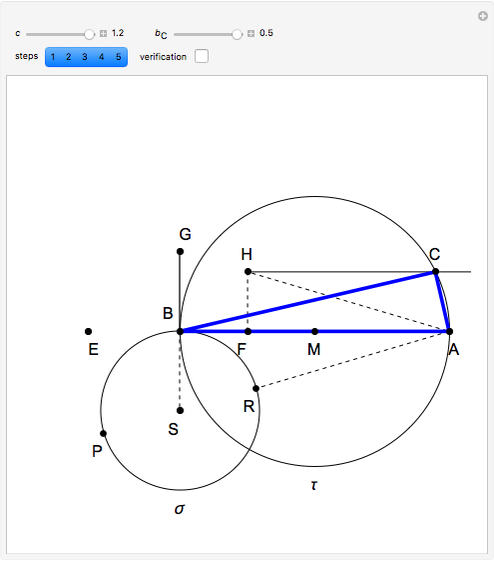
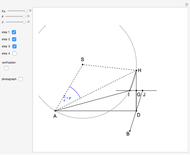
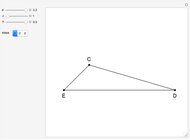
Step 5. Draw the triangle  .
.
Verification
From step 1,  .
.
Step 4 and Thales's theorem imply that triangle  is right-angled at
is right-angled at  .
.
It remains to prove that the length of the angle bisector at  is
is  .
.
Theorem 1. Let  be a point on the hypotenuse
be a point on the hypotenuse  , and let
, and let  and
and  be the perpendicular projections of
be the perpendicular projections of  on
on  and
and  , respectively. Then the rectangle
, respectively. Then the rectangle  is a square if and only if
is a square if and only if  is the angle bisector at
is the angle bisector at  .
.
Proof. If  is a square, then the diagonal
is a square, then the diagonal  forms angles
forms angles  with
with  and
and  , so it bisects the angle
, so it bisects the angle  at
at  .
If
.
If  is the angle bisector at
is the angle bisector at  , then
, then  and
and  are equilateral right-angled congruent triangles and therefore
are equilateral right-angled congruent triangles and therefore  . So
. So  is a square. \[FilledSquare]
is a square. \[FilledSquare]
Theorem 2. Let  be a right triangle with hypotenuse
be a right triangle with hypotenuse  , legs
, legs  and
and  , and where the length of the angle bisector is
, and where the length of the angle bisector is  . Then
. Then  is a solution of the equation
is a solution of the equation  , and the altitude
, and the altitude  is given by
is given by  .
.
Proof. Let  be the angle bisector at
be the angle bisector at  with
with  on
on  and let
and let  be as described in Theorem 1. The side length of the square is
be as described in Theorem 1. The side length of the square is  , since
, since  is the length of its diagonal. We can express twice the area of the triangle
is the length of its diagonal. We can express twice the area of the triangle  as
as  . Since
. Since  , we have a quadratic equation for
, we have a quadratic equation for  , namely,
, namely,  or
or  .
Twice the area of
.
Twice the area of  is
is  so
so  . \[FilledSquare]
. \[FilledSquare]
The first equation of theorem 2 gives a construction of  using the power of
using the power of  with respect to
with respect to  . In this case, by step 2,
. In this case, by step 2,  , since
, since  .
.
The second equation of theorem 2 gives a construction of  using similarity of triangles. Namely, by step 3,
using similarity of triangles. Namely, by step 3,  is such that
is such that  is similar to
is similar to  . So
. So  from
from  .
.
Since  is a right triangle with hypotenuse
is a right triangle with hypotenuse  and altitude
and altitude  , using theorem 2,
, using theorem 2,  .
.
[less]

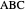 given the length
given the length  of the hypotenuse
of the hypotenuse 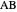 and the length of the angle bisector
and the length of the angle bisector 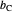 at
at 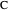 . Let
. Let 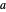 and
and  be the length of the legs.
be the length of the legs.