A Perfect Cognac Glass

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
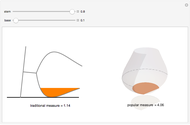
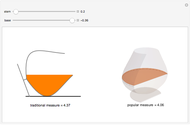
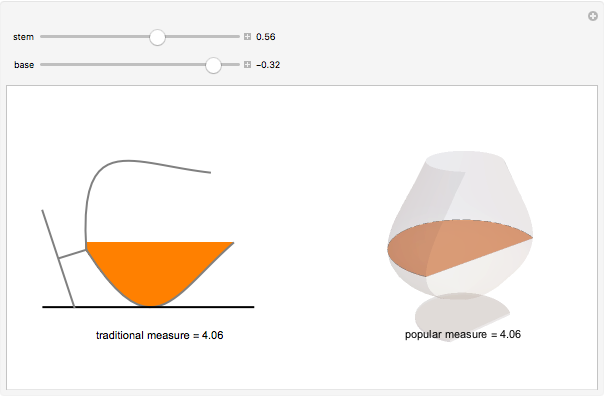
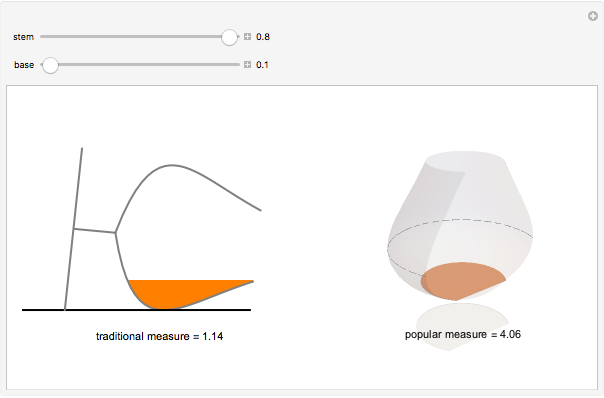
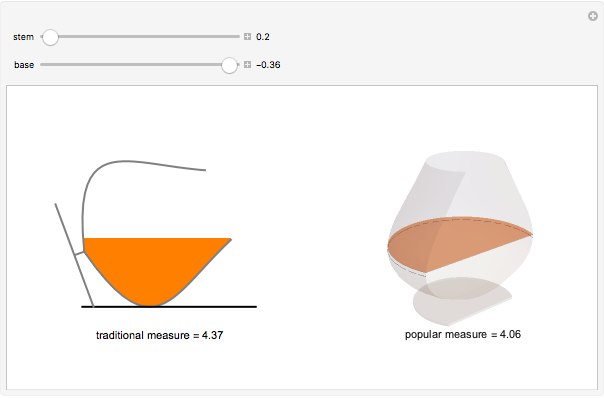
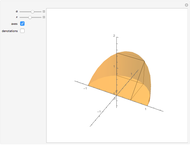
The traditional measure of cognac is to place the glass on its side and fill to the brim. An equally popular measure is to place the glass vertically and fill to point of maximum surface area. For a given glass curvature and stem length, by adjusting the base width we can create the perfect cognac glass, where the two measures are equal. Varying the stem length will adjust the base so that the measure is not changed.
Contributed by: Liam Cleary (January 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The cognac glass is described by its radial function 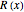 , where
, where  is the height when the glass is sitting on its base. In order to calculate the traditional measure of cognac (when the glass is placed on its side), we need the area enclosed by the chord
is the height when the glass is sitting on its base. In order to calculate the traditional measure of cognac (when the glass is placed on its side), we need the area enclosed by the chord 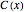 created by the cognac level
created by the cognac level 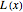 . That area is simply the area of its sector minus the area of its isosceles triangle. The volume is then equal to the integral over
. That area is simply the area of its sector minus the area of its isosceles triangle. The volume is then equal to the integral over 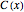 from 0 to
from 0 to 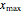 (the brim of the glass), and depending on
(the brim of the glass), and depending on 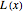 , we must switch between the upper and lower areas enclosed by the chord. The popular measure of cognac (when the glass is placed standing up) is simply
, we must switch between the upper and lower areas enclosed by the chord. The popular measure of cognac (when the glass is placed standing up) is simply 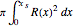 , where
, where 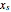 is the point of maximum surface area.
is the point of maximum surface area.
Permanent Citation
"A Perfect Cognac Glass"
http://demonstrations.wolfram.com/APerfectCognacGlass/
Wolfram Demonstrations Project
Published: January 25 2013