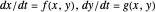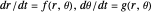A Tour of Second-Order Ordinary Differential Equations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
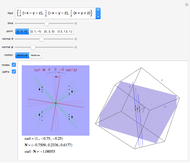
This Demonstration is a tour of autonomous second-order ordinary differential equations (ODEs). The systems chosen represent most of the possible important qualitative behaviors. The general form of a second-order ODE is:
[more]
Contributed by: Brian Vick (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Some of the characteristics of the systems of ODEs selected for this tour are described. These insights suggest interesting explorations.
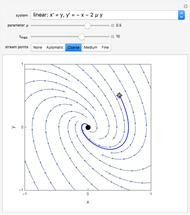
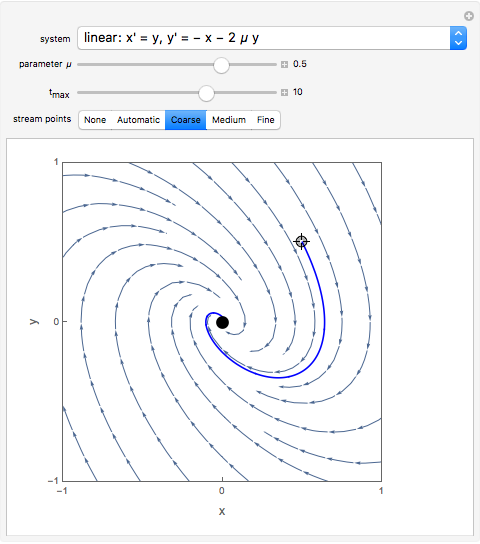
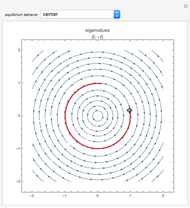
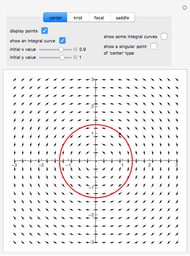
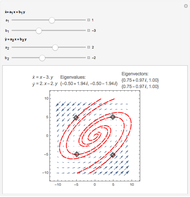
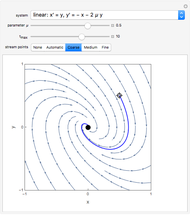
For the linear system, 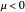 produces an unstable spiral,
produces an unstable spiral, 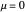 is a center, and
is a center, and 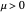 produces a stable spiral.
produces a stable spiral.
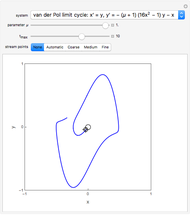
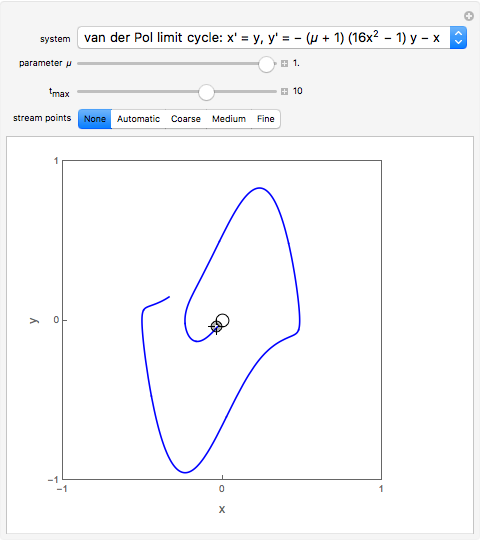
For the van der Pol equation, 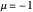 reduces to a linear center. As
reduces to a linear center. As  increases, a limit cycle forms.
increases, a limit cycle forms.
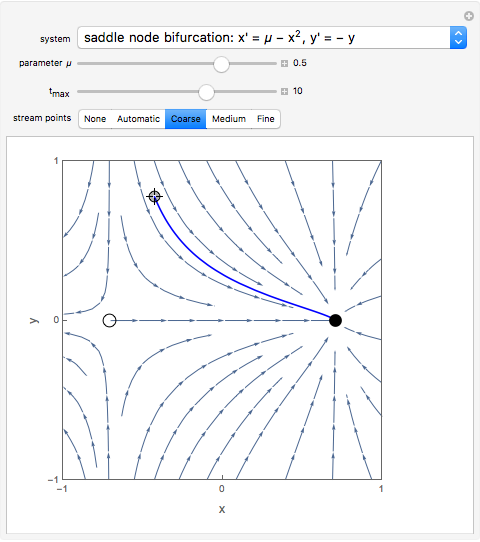
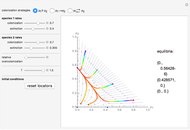
The critical value of the parameter  for all the bifurcation cases occurs at
for all the bifurcation cases occurs at 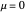 , where the number and stability of the fixed points change, causing a qualitatively different dynamical picture.
, where the number and stability of the fixed points change, causing a qualitatively different dynamical picture.
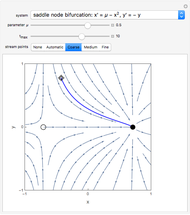
The saddle node has no fixed points for 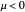 and fixed points at
and fixed points at 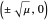 for
for 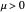 .
.
The transcritical fixed points at 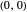 and
and 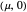 switch stability at
switch stability at 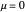 .
.
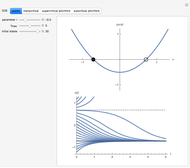
The supercritical pitchfork has one stable fixed point at 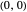 for
for 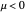 . When
. When 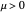 ,
, 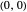 becomes unstable and a pair of symmetric stable points forms at
becomes unstable and a pair of symmetric stable points forms at 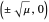 .
.
The subcritical pitchfork has a stable fixed point at 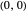 and a symmetric pair of unstable points at
and a symmetric pair of unstable points at 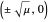 for
for 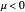 . When
. When 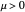 ,
, 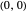 becomes unstable and all trajectories diverge.
becomes unstable and all trajectories diverge.
For both the supercritical and subcritical Hopf cases, the origin is a stable spiral when 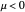 and bifurcates to an unstable spiral when
and bifurcates to an unstable spiral when 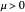 . When
. When 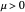 , the trajectories approach limit cycles.
, the trajectories approach limit cycles.
Reference:
S. H. Strogatz, Nonlinear Dynamics and Chaos, Jackson, TN: Perseus Books Publishing, 1994.
Permanent Citation