Adaptive Monte Carlo Integration

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
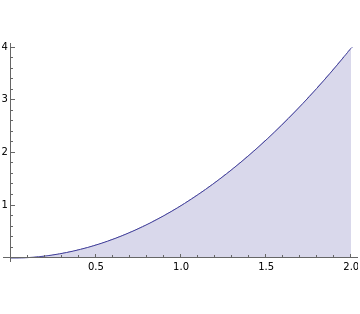
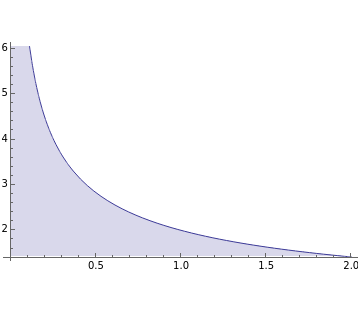
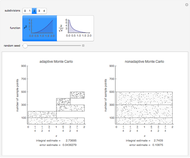
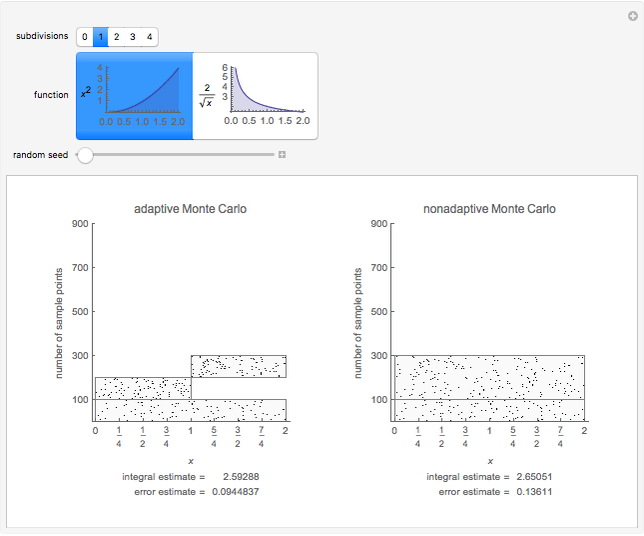
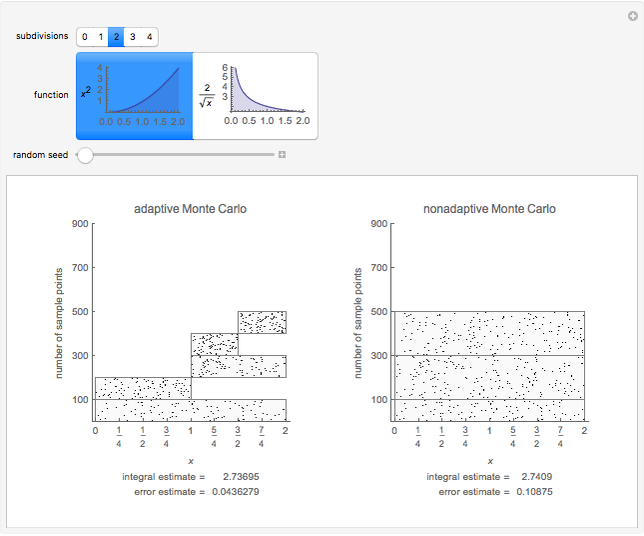
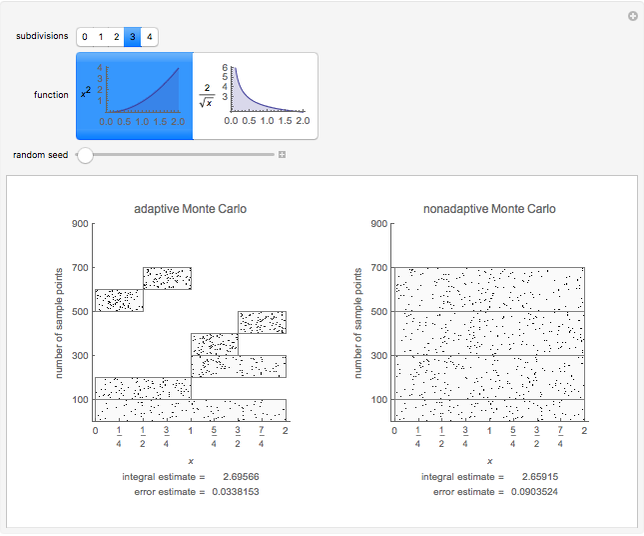
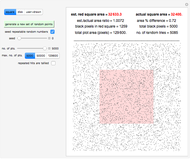
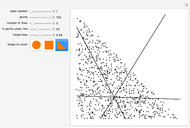
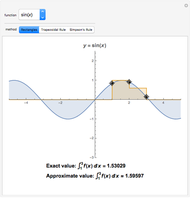
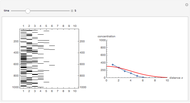
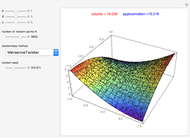
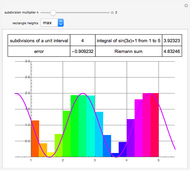
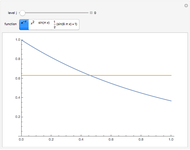
This Demonstration compares adaptive and nonadaptive Monte Carlo integration for two different functions, 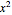 and
and 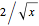 . The plot shows the places on the interval
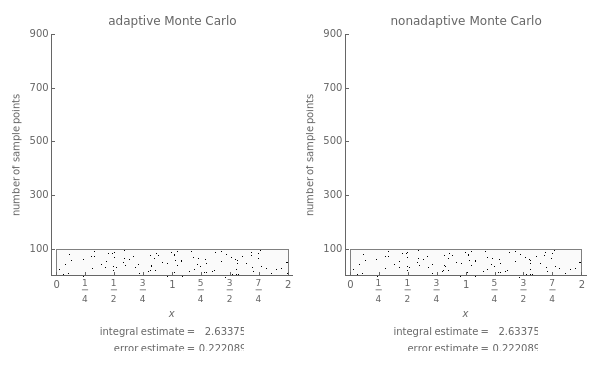
. The plot shows the places on the interval 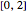 where sample points are added as the number of sample points is increased. The actual values of the integrals to six significant figures are 2.66667 and 5.65685. The adaptive technique generally gets better estimates with the same number of sample points by subdividing the subinterval with the highest error estimate. Normally this process would be repeated until some error criterion is satisfied, but in this Demonstration only four subdivisions are shown.
where sample points are added as the number of sample points is increased. The actual values of the integrals to six significant figures are 2.66667 and 5.65685. The adaptive technique generally gets better estimates with the same number of sample points by subdividing the subinterval with the highest error estimate. Normally this process would be repeated until some error criterion is satisfied, but in this Demonstration only four subdivisions are shown.
Contributed by: Sijia Liang and Bruce Atwood (January 2013)
(Beloit College)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In one dimension, if 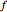 is integrable on the interval
is integrable on the interval 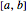 , then the average value of
, then the average value of 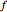 is
is 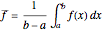 . From this, the nonadaptive (basic) Monte Carlo method estimates the integral by
. From this, the nonadaptive (basic) Monte Carlo method estimates the integral by 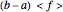 , where
, where 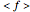 is the mean of the function evaluated at
is the mean of the function evaluated at  randomly sampled points. The corresponding error estimate is
randomly sampled points. The corresponding error estimate is 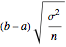 , where
, where 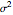 is the variance of the function evaluations. Thus the error can be reduced by increasing the number of sample points or reducing the variance. The key idea of adaptive Monte Carlo is to reduce the variance by recursive subdivision. Parts of this Demonstration are modifications of examples from the Wolfram Mathematica Documentation Center tutorial "Advanced Numerical Integration in Mathematica" (see link below). Students should try to explain why Monte Carlo integration has more difficulty for the function with the singularity at 0. (Hint: look at the formulas for the integral estimate and error estimate.)
is the variance of the function evaluations. Thus the error can be reduced by increasing the number of sample points or reducing the variance. The key idea of adaptive Monte Carlo is to reduce the variance by recursive subdivision. Parts of this Demonstration are modifications of examples from the Wolfram Mathematica Documentation Center tutorial "Advanced Numerical Integration in Mathematica" (see link below). Students should try to explain why Monte Carlo integration has more difficulty for the function with the singularity at 0. (Hint: look at the formulas for the integral estimate and error estimate.)
Permanent Citation