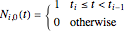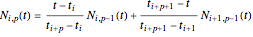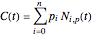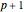Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

B-Spline Curve with Knots

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

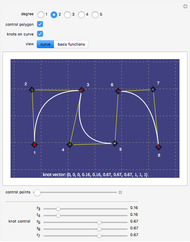
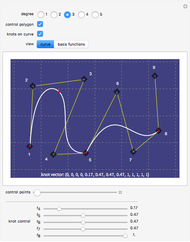
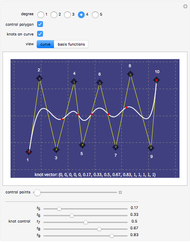
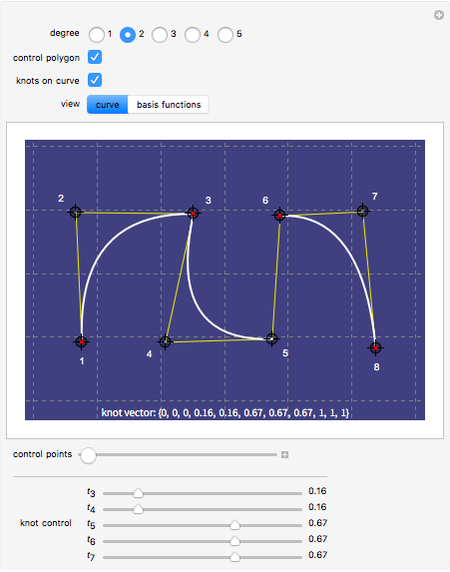
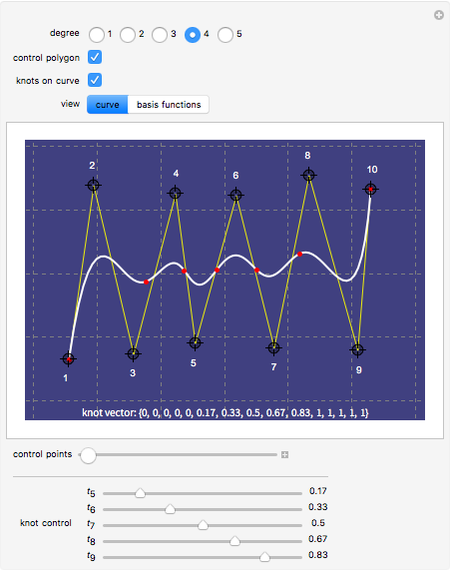
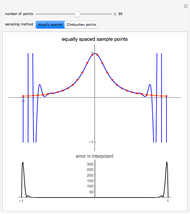
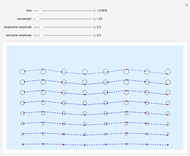
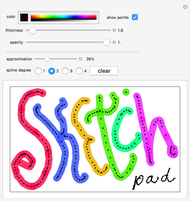
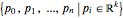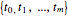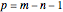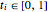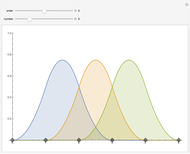
This Demonstration illustrates the relation between B-spline curves and their knot vectors. Start with the control points and a knot vector , where the degree of the B-spline is . The knot vector satisfies and 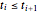. The B-spline basis functions are defined as:

[more]

,

and a B-spline curve is defined as:

.

For nonperiodic B-splines, the first knots are equal to 0 and the last knots are equal to 1. If duplication happens at the other knots, the curve becomes times differentiable. So, by overlapping the knots, you can generate a curve with sharp turns or even discontinuities.

When the number of control points is , the basis functions are reduced to Bernstein polynomial, thus the curve becomes a Bézier curve.

[less]

Contributed by: Yu-Sung Chang (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Red points indicate the knot points 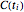on the curve. Hold down the Alt key and click to add new control points (up to 12). Changes in degree and number of control points will cause the knot vector to be recomputed.

Choose "view basis functions" to show the B-spline basis functions of a given knot vector instead of the B-spline curve.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send