Details

The unit-rod polyhedron shows a rod between all vertex pairs a unit distance apart.

The unit-star picture builds polygons from half-unit rods meeting at a vertex.

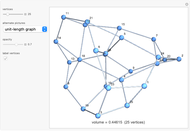
The unit-length graph shows how vertices a unit distance apart are connected.

The planar vertex map puts the vertices on a sphere, then unrolls the sphere into a planar form.

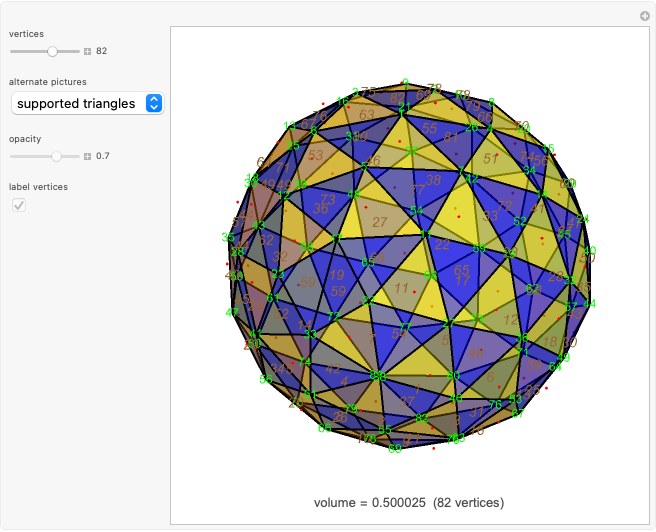
In the supported triangles image, all vertices of a blue triangle (with brown number) are at distance 1 from an opposing vertex with a matching green number.

The Initialization section contains various programs that may be able to improve some of the solutions.

References

[1] B. Kind and P. Kleinschmidt, "On the Maximal Volume of Convex Bodies with Few Vertices," Journal of Combinatorial Theory, Series A, 21(1) 1976 pp. 124–128. doi:10.1016/0097-3165(76)90056-X.

[2] A. Klein and M. Wessler, "The Largest Small -dimensional Polytope with Vertices," Journal of Combinatorial Theory, Series A, 102(2), 2003 pp. 401–409. doi:10.1016/S0097-3165(03)00054-2.

[3] A. Klein and M. Wessler, "A Correction to 'The Largest Small -dimensional Polytope with Vertices,'" Journal of Combinatorial Theory, Series A, 112(1), 2005 pp. 173–174. doi:10.1016/j.jcta.2005.06.001.

[4] E. Pegg Jr. "Biggest Little Polyhedra" from Wolfram Community—A Wolfram Web Resource. (Oct 28, 2015) community.wolfram.com/groups/-/m/t/463699.

[5] E. Pegg Jr. "Biggest Little Polyhedron—New Solutions in Combinatorial Geometry" from Wolfram Blog—A Wolfram Web Resource. (May 20, 2015) blog.wolfram.com/2015/05/20/biggest-little-polyhedronnew-solutions-in-combinatorial-geometry.