Center of an Equilateral Triangle Circumscribing a Given Parabola

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
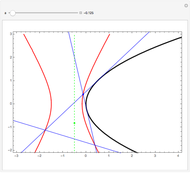
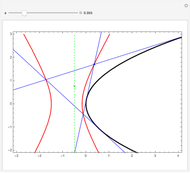
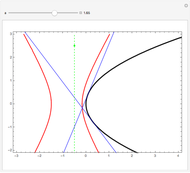
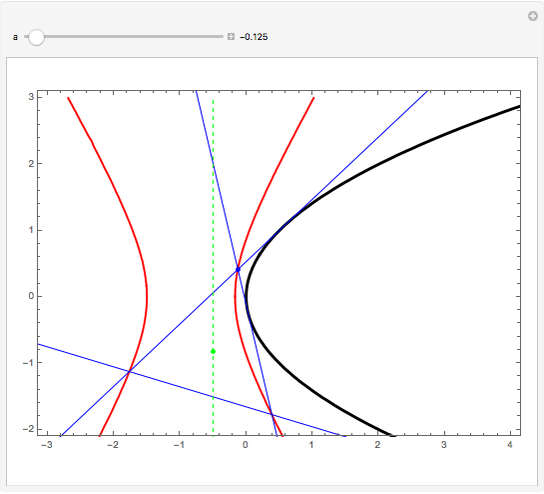
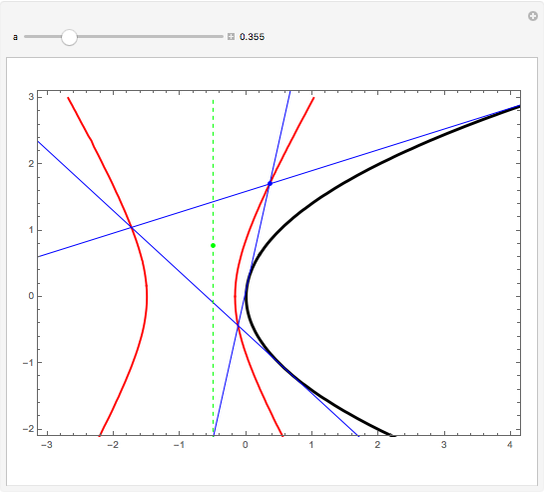
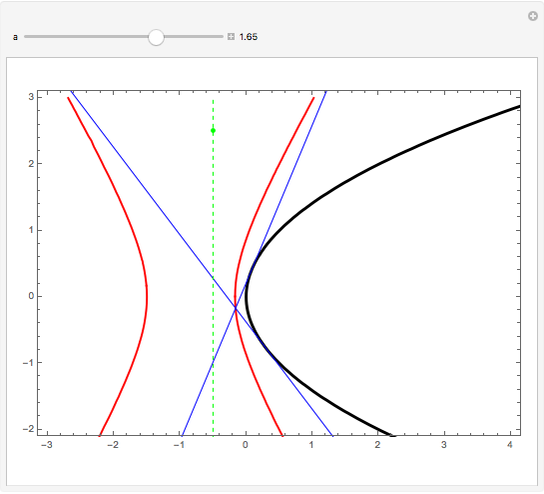
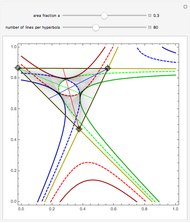
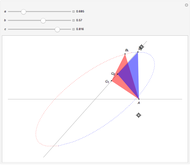
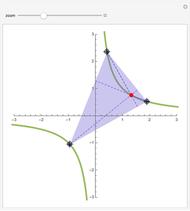
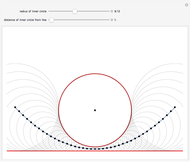
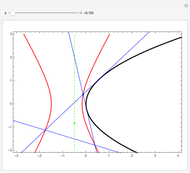
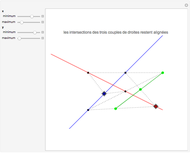
If an equilateral triangle circumscribes a parabola, that is, its sides (extended if necessary) are tangent to the parabola, then its center moves along a straight line, which is none other than the parabola's directrix. To prove this was a question in the oral examination of the Ecole Polytechnique in 1928.
Contributed by: Emmanuel Amiot (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
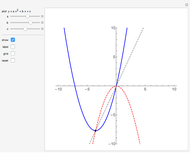
A parabola is the locus of points equidistant from a given point (the focus) and a given line (the directrix). A proof could be obtained from projective geometry, where the tangents to the parabola themselves define a conic section in another space. But Mathematica computes the coordinates of the vertices and center of the triangle easily enough, starting from any tangent to the parabola. As a bonus, the computation yields that the vertices of this triangle are located on a hyperbola (see the blue dot on the red curve and observe the other vertices of the triangle).