Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

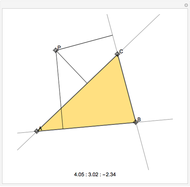
Circumcircles of Two Midpoints and an Altitude

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

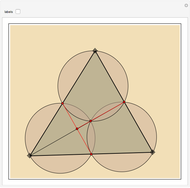
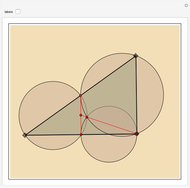
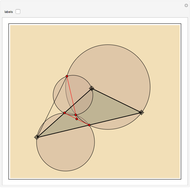
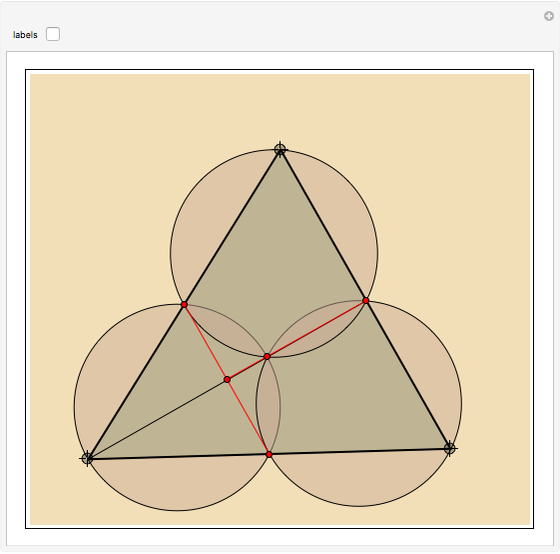
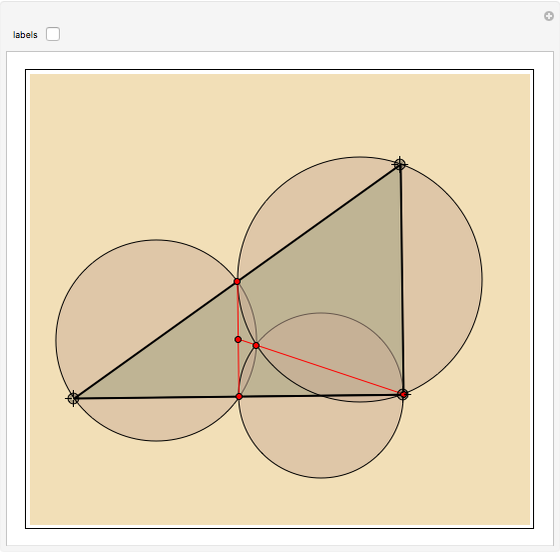
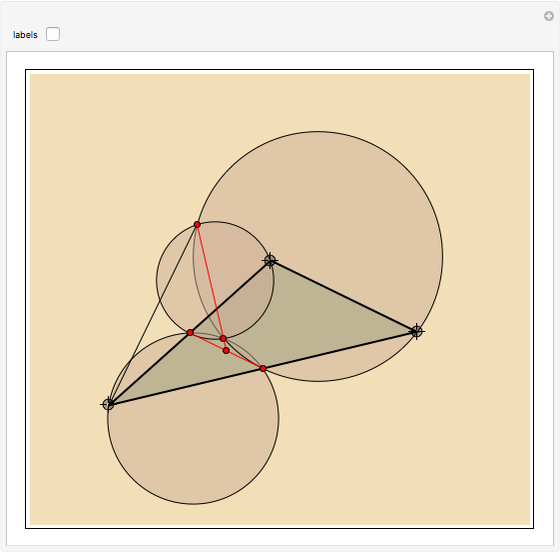
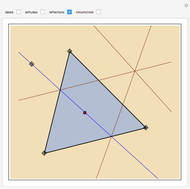
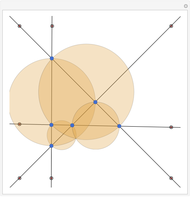
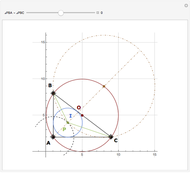
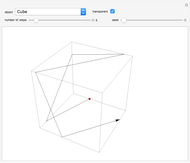
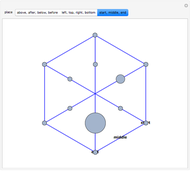
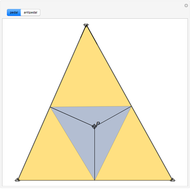
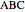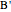In the triangle let and 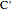be the midpoints of the sides 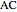and 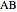and let 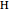be the foot of the altitude from 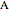to 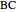. Prove that the circumcircles of the triangles 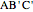, , 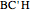and 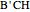have a common point 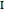and that the line 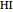passes through the midpoint of the segment .

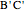Contributed by: Jaime Rangel-Mondragon (July 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

This Demonstration comes from problem 6 of the shortlisted problems for the 1970 International Mathematical Olympiad (IMO).

Reference

[1] D. Djukić, V. Janković, I. Matić, and N. Petrović, The IMO Compendium, 2nd ed., New York: Springer, 2011 p. 69.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send