Cold Wave Plasma Dispersion

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
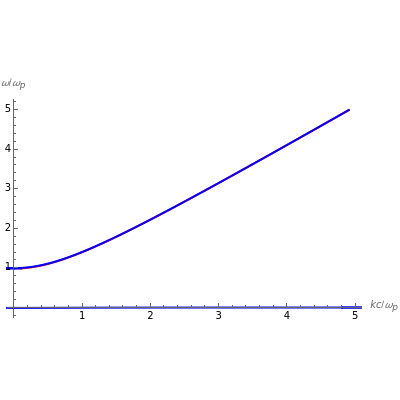
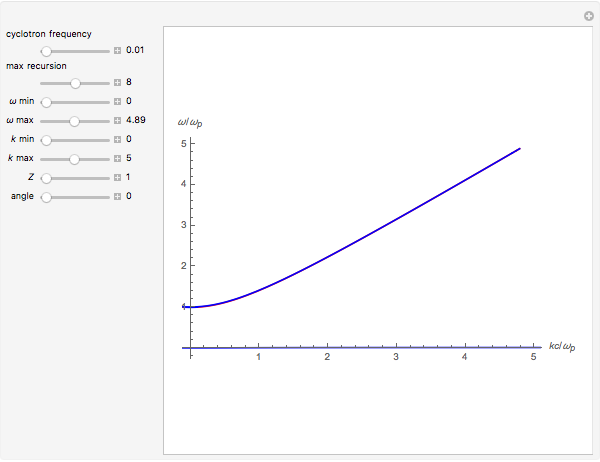
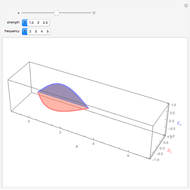
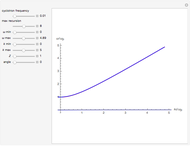
This Demonstration solves for the dielectric tensor in the cold plasma wave dispersion relation, which determines the frequency as a function of wavenumber for waves independent of temperature in a plasma. All frequencies are normalized to the electron plasma frequency. The variable 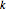 is the wavenumber in units of
is the wavenumber in units of 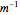 . In the graph,
. In the graph,  is scaled to
is scaled to 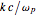 and
and  is scaled to
is scaled to 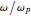 , where
, where 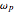 is the electron plasma frequency.
is the electron plasma frequency.
Contributed by: Ken Flanagan (October 2011)
Open content licensed under CC BY-NC-SA
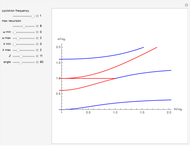
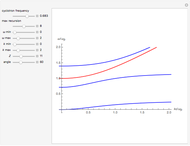
Snapshots
Details
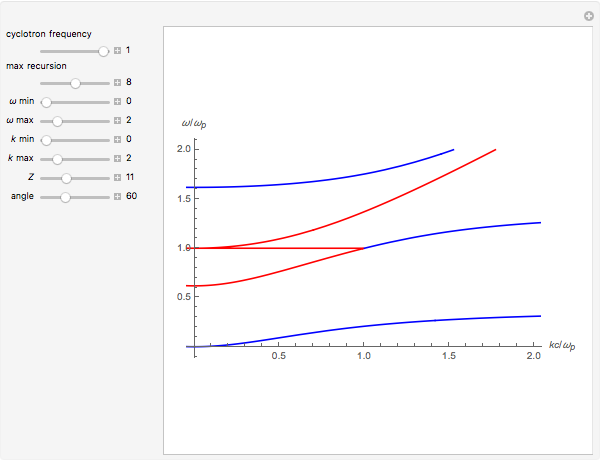
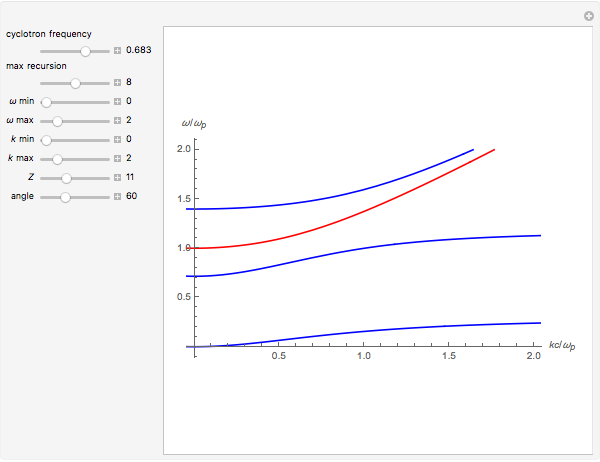
The variable 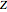 is the atomic number of the ions (1–30 in this Demonstration).
is the atomic number of the ions (1–30 in this Demonstration).
Change " min", "
min", " max", "
max", " min", and "
min", and " max" to vary the area of the dispersion plot being solved for (i.e., acts as the bounds for the solution to the dielectric tensor).
max" to vary the area of the dispersion plot being solved for (i.e., acts as the bounds for the solution to the dielectric tensor).
The variable "angle" refers to the angle that the wave makes with the magnetic field in degrees.
The variable "max recursions" defines the precision of the plot, but a higher value takes longer.
For computational reasons, the cyclotron frequency cannot be set to 0, so it is bound between .01 and 1 times the electron plasma frequency.
The red curves correspond to the solutions found by taking the plus sign in the plasma dispersion equation and the blue correspond to the solutions found by taking the minus sign.
References
[1] R. J. Goldston, "Low-Frequency Waves in a Magnetized Plasma," Introduction to Plasma Physics, London: Institute of Physics Publishing, 1995 pp. 285–308.
[2] P. M. Bellan, "Cold Plasma Waves in a Magnetized Plasma," Fundamentals of Plasma Physics, New York: Cambridge University Press, 2006 pp. 206–241.
For more information on plasma waves, see the Wikipedia entry for "Plasma waves".
For more information on dispersion relations in general, see the Wikipedia entry for "Dispersion relation".
Permanent Citation