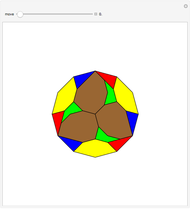
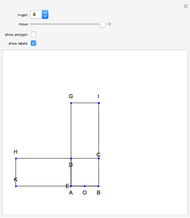
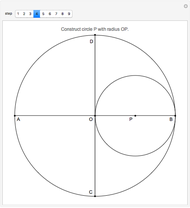
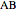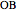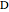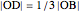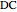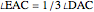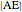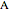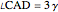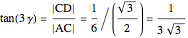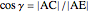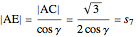Constructing a Regular Heptagon Using Plemelj's Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
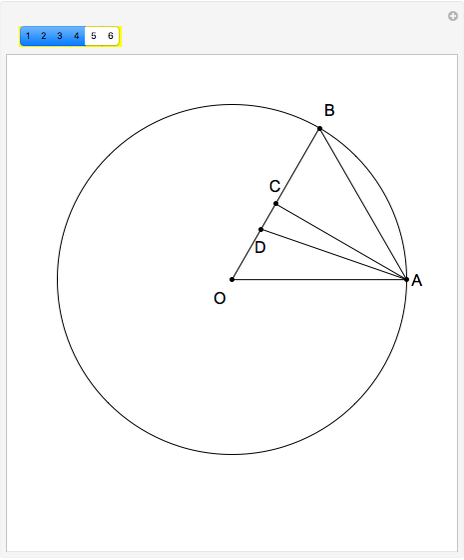
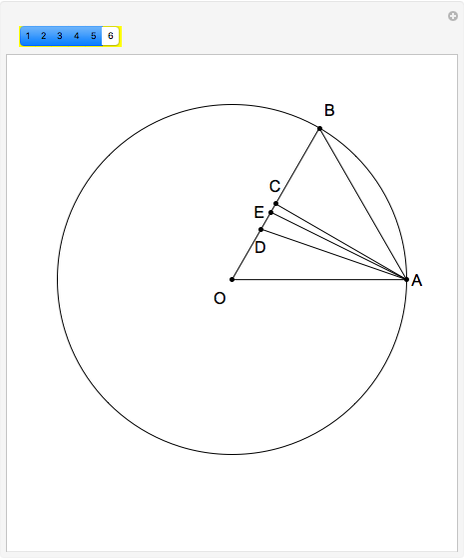
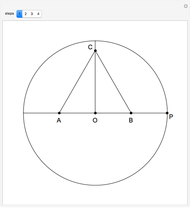
This Demonstration shows Plemelj's method for constructing a regular heptagon, using the following steps:
[more]
Contributed by: Izidor Hafner (September 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This method for constructing a regular heptagon using angle trisection was found by Plemelj in 1892 and published in 1912. The construction is taken from [1, pp. 183–184]. The approximation
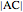 for
for 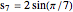 was known to Abûl-Wefâ and Heron of Alexandria [1, p. 184].
was known to Abûl-Wefâ and Heron of Alexandria [1, p. 184].
Start with the trigonometric identity
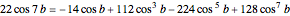 .
.
Since
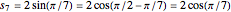 ,
,
replace  by
by 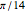 and
and 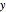 by
by 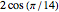 in the trigonometric identity to get the cubic
in the trigonometric identity to get the cubic
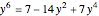 .
.
Then
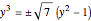 .
.
Since 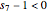 and
and 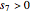 , take
, take 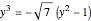 .
.
Substitute 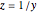 to get
to get
 .
.
Substitute 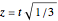 to get the Vieta form of the equation,
to get the Vieta form of the equation,
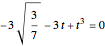 .
.
Set
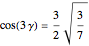
to get the positive solutions
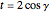 ,
,
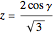 ,
,
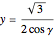 .
.
So
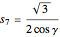 ,
,
where
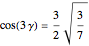 .
.
Then
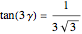 .
.
Reference
[1] G. E. Martin, Geometric Constructions, New York: Springer, 1998.
Permanent Citation