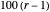Details

For efficiency, we compute where is the Euler totient function [5], and precompute the inside sum [7].

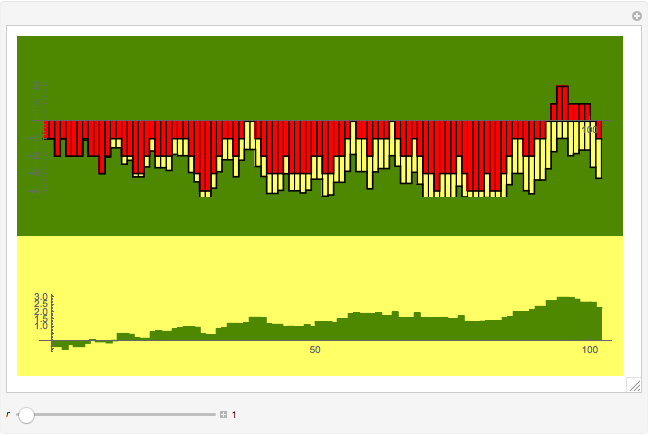
In all, values of the Mertens function are plotted as red bars in intervals of 100 per visual frame [6].

Corresponding values of the distribution measure 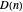are overlaid in yellow to compare the two function values.

Where one colored bar hides the other fully, use the difference plotted below as green bars to compare values.

For , the heights of the red and yellow bars show correlations and patterns as expected from mappings that exist between the Möbius function and subsets of the Farey sequence with denominators [4].

For , [4], suggesting observable patterns continuing to this range.

In [4], it is seen from Ramanujan's sums that , where runs over the set .

Let ; then binds the two functions.

The distribution of the primes gives the distribution of the Farey sequence via the prime reciprocals.

The distribution of the Möbius function and its summation, the Mertens function, have mysterious random-like properties.

References

[1] Wikipedia. "Möbius Function." (Jun 17, 2013) en.wikipedia.org/wiki/Mobius_function.

[2] Wikipedia. "Mertens Function." (May 3, 2013) en.wikipedia.org/wiki/Mertens_function.

[3] Wikipedia. "Farey Sequence." (Jun 9, 2013) en.wikipedia.org/wiki/Farey_sequence.

[4] J. Vondra. "Experimenting with Sums of Primitive Roots of Unity" from the Wolfram Demonstrations Project. demonstrations.wolfram.com/ExperimentingWithSumsOfPrimitiveRootsOfUnity.

[5] Wikipedia. "Euler's Totient Function." (Sep 18, 2013) en.wikipedia.org/wiki/Euler’s_totient _function.

[6] S. Wolfram. "Mertens Conjecture" from the Wolfram Demonstrations Project. demonstrations.wolfram.com/MertensConjecture.

[7] L. Quet, "Sum of Positive Integers, k, where k <= n/2 and GCD(k,n)=1." (Jan 20, 2002) oeis.org/A066840.