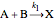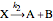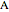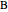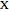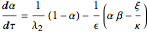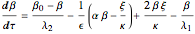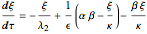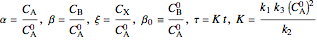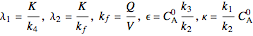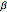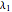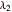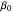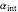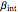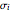This Demonstration treats isothermal oscillatory reactions that can occur in a continuously stirred tank reactor (CSTR). The kinetic scheme for the autocatalytic reaction involves a series of successive bimolecular steps that are chemically and thermodynamically realistic. They are self-consistent stoichiometrically (mass conserving) and obey detail balancing of thermodynamics [1]:
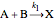 ,
, 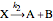 ,
, 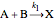 ,
, 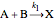 .
.
The dimensionless species balances for 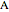 ,
, 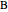 , and
, and 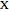 in a CSTR are:
in a CSTR are:
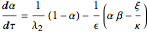 ,
, 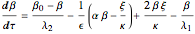 ,
, 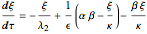 ,
,
where the dimensionless variables are defined as
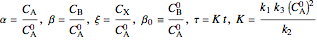 ,
, 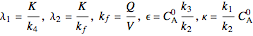 .
.
In this model  ,
, 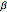 , and
, and  are dimensionless molar concentrations for species
are dimensionless molar concentrations for species 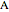 ,
, 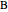 , and
, and 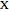 . There are five dimensionless parameters that determine the dynamics of the reactor:
. There are five dimensionless parameters that determine the dynamics of the reactor: 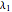 ,
, 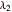 ,
,  , and
, and  are dimensionless rate constants, and
are dimensionless rate constants, and 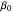 is the concentration ratio of species
is the concentration ratio of species 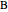 to species
to species 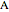 entering the reactor. Also of interest are the initial concentrations of species
entering the reactor. Also of interest are the initial concentrations of species 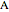 and
and 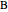 in the reactor at start-up,
in the reactor at start-up, 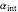 and
and 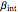 .
.
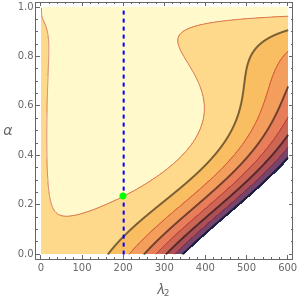
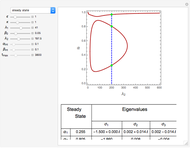
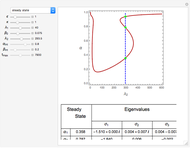
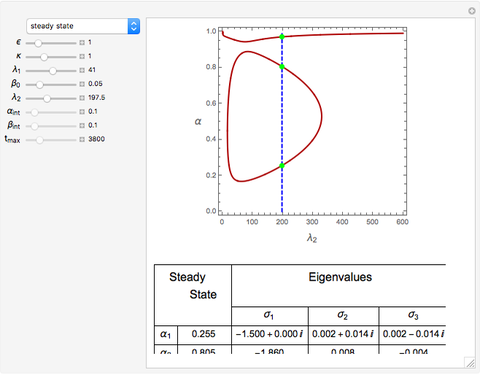
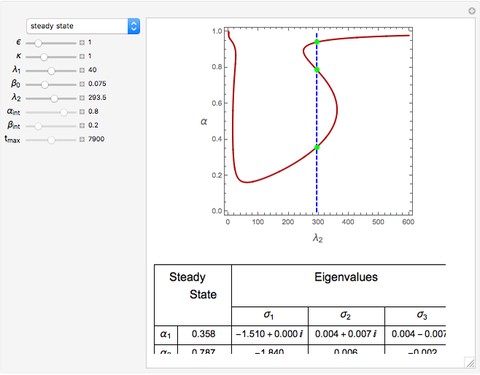
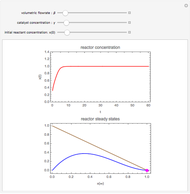
Depending on the choice of parameters, the reactor can have multiple steady states, which are conveniently represented by plotting  versus
versus 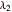 . By selecting the steady state tab from the drop-down menu, you can view how the portrait of steady states is altered by changing the parameter values using the sliders. Of particular interest is the existence of an isola (most easily found by decreasing
. By selecting the steady state tab from the drop-down menu, you can view how the portrait of steady states is altered by changing the parameter values using the sliders. Of particular interest is the existence of an isola (most easily found by decreasing 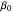 ). An isola is an isolated branch of steady state solutions.
). An isola is an isolated branch of steady state solutions.
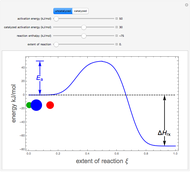
A linear stability analysis of the steady states is determined by computing the eigenvalues 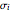 for each steady state. A steady state is unstable if any one of three associated eigenvalues has a positive real part. For each choice of
for each steady state. A steady state is unstable if any one of three associated eigenvalues has a positive real part. For each choice of 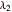 the steady state values of
the steady state values of  with the associated eigenvalues are shown in a table below the
with the associated eigenvalues are shown in a table below the  versus
versus 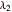 plot.
plot.
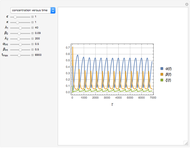
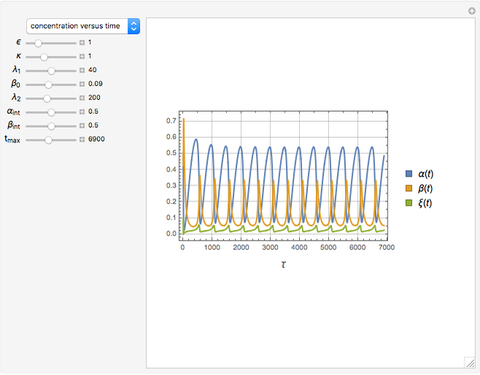
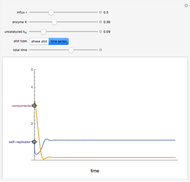
The onset of oscillatory behavior occurs when a complex eigenvalue crosses the imaginary axis (Hopf bifurcation). In this Demonstration there is a single Hopf bifurcation. By selecting the concentration versus time in the drop-down menu, you can examine the oscillatory behavior for appropriate values of 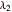 .
.
When an isola is present is it possible to have multiple stable steady states. By selecting different values of 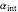 and
and 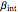 , you can find the basin of attraction for each of the stable steady states for the selected value of
, you can find the basin of attraction for each of the stable steady states for the selected value of 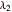 .
.
[less]