Cunningham's Simply Connected Kakeya Set

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
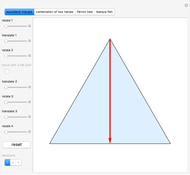
The Kakeya problem seeks the smallest convex region in which a unit segment can be moved back to itself but in the opposite direction. The answer is an equilateral triangle of unit height [3].
[more]
Contributed by: Izidor Hafner (August 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Given two parallel lines, a Pál joint lets you move a unit line segment continuously from one to the other through a set of arbitrarily small area.
A Kakeya set (or Besicovitch set) is one that can contain a unit segment in any direction.
A Kakeya needle set is a set through which a line segment can be moved continuously back to itself but turned 180°. (Thus a Kakeya needle set is a Kakeya set.)
Cunningham [7] proved the following theorem:
Given  , there exists a simply connected Kakeya set of area less than
, there exists a simply connected Kakeya set of area less than  contained in a circle of radius 1.
contained in a circle of radius 1.
See Besicovitch's talk [5] and expository article [6].
References
[1] Wikipedia. "Kakeya Set." (Aug 8, 2016) en.wikipedia.org/wiki/Kakeya_set.
[2] K. J. Falconer, The Geometry of Fractal Sets, 1st ed., Cambridge: Cambridge University Press, 1990.
[3] D. Wells, The Penguin Dictionary of Curious and Interesting Geometry, London: Penguin Books, 1991.
[4] Kakeya's Needle Problem [Video]. (Aug 8, 2016) www.youtube.com/watch?v=j-dce6QmVAQ.
[5] The Kakeya Problem [Video]. (Aug 8, 2016) av.cah.utexas.edu/index.php?title=Category:The_Kakeya_Problem.
[6] A. S. Besicovitch, "The Kakeya Problem," The American Mathematical Monthly, 70, 1963 pp. 697–706.
[7] F. Cunningham, Jr., "The Kakeya Problem for Simply Connected and for Star-shaped Sets," The American Mathematical Monthly, 78, 1971 pp. 114–129. www.maa.org/sites/default/files/pdf/upload_library/22/Ford/Cunningham.pdf
Permanent Citation
"Cunningham's Simply Connected Kakeya Set"
http://demonstrations.wolfram.com/CunninghamsSimplyConnectedKakeyaSet/
Wolfram Demonstrations Project
Published: August 9 2016