De Finetti's Game

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Bruno de Finetti defined probability as a quantity that measures a subjective degree-of-belief rather than an objective quantity. According to de Finetti, such a (possibly very vague) degree-of-belief can be quantified through thought experiments involving urns with a varying fraction of differently colored balls. A degree-of-belief value is quantified by the willingness of people to risk money by betting on the result of randomly drawing a ball of a particular color.
Contributed by: Frank Scherbaum (January 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
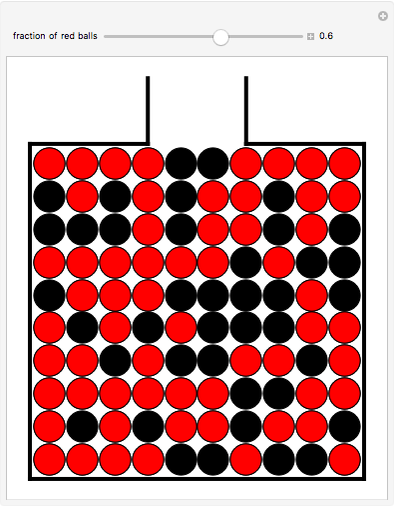
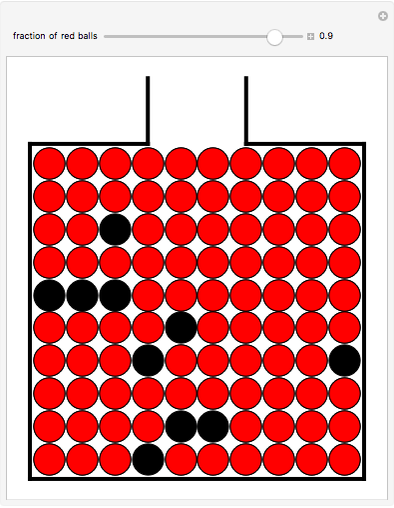
Assume you have taken an exam and you want to express your degree-of-belief that you have passed as a subjective probability value. In the de Finetti game you are confronted with the urn above, containing a mixture of red and black balls. Subsequently, you are given two options.
Option 1: You randomly have a ball selected from that urn. If it turns out to be red, you will get €1000, while if it turns out to be black, you will have to pay the same amount.
Option 2: You wait until the result of the exam is revealed. If you pass, you will get €1000, while if you fail, you will have to pay the same amount.
If, looking at the urn, you choose option 1, your subjective probability estimate for passing must be less than the slider value. If you choose option 2, your subjective probability value must be larger than the slider value. You then increase the number of red balls in the urn by moving the slider to the right until the chances to win (or lose) money seem equally likely for options 1 and 2. The resulting fraction of red balls is your subjective probability value for passing the exam.
Reference
[1] B. de Finetti, Theory of Probability: A Critical Introductory Treatment, Vol. 1 (A. MachiÌ and A. Smith, trans.), New York: Wiley, 1974.
Permanent Citation
"De Finetti's Game"
http://demonstrations.wolfram.com/DeFinettisGame/
Wolfram Demonstrations Project
Published: January 25 2013