Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

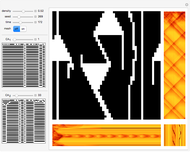
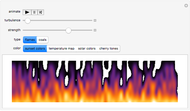
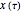Digital Representation of a Nonlinear ODE with Small Differences in Initial Conditions

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

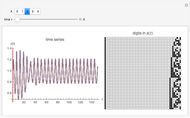
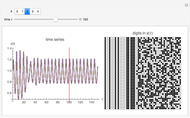
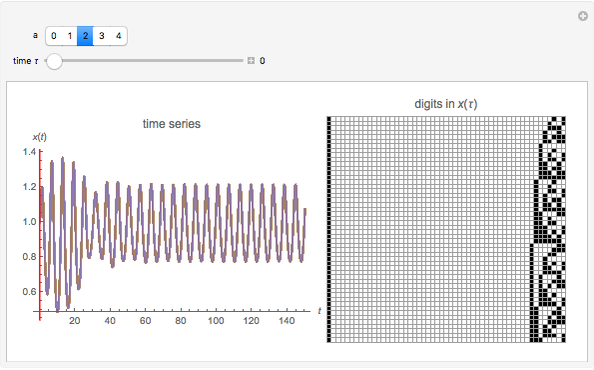
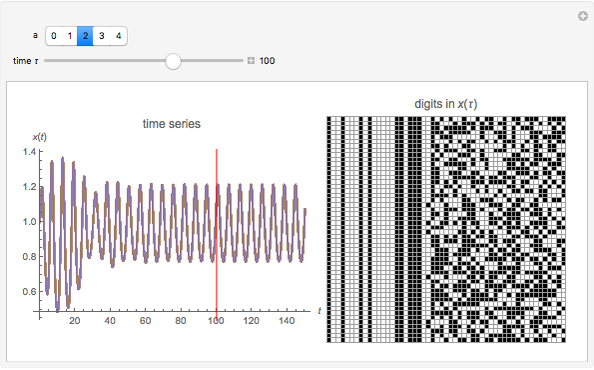
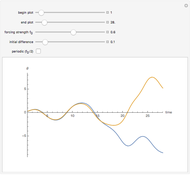
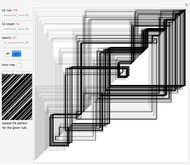
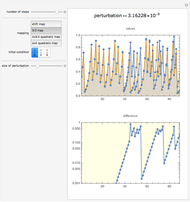
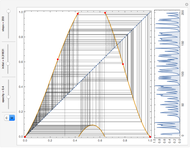
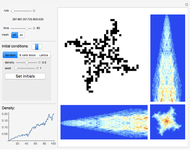
The graphic on the left overlays the plots of the solutions 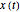of a nonlinear ODE with 50 slightly different initial conditions.

[more]

The graphic on the right shows the digits of in base 2 for each of those solutions at . (The line is shown in red on the left.) Each row represents one of the 50 solutions.

Thus this Demonstration shows the change in the digital representation of the solutions to that set of nonlinear ODEs at a point as the ODE changes from periodic to chaotic with increasing .

[less]

Contributed by: Stella Chuyue Dong and Vitaliy Kaurov (December 2012)
Created at the 2011 NKS Summer School (NKS|Online)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Given a nonlinear ODE of the form 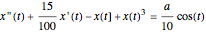, where 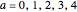, this Demonstration evolves the equation in time, assuming initial 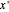to be fixed.

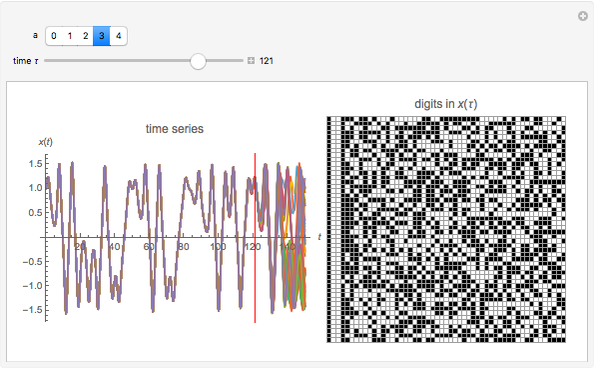
With the advent of chaos (obtained by increasing the forcing parameter ), the digital representation loses its coherence, indicating a divergence between the solutions proportional to its Lyapunov measure.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send