Disk with a Hole Rolling in a Semicircular Well

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
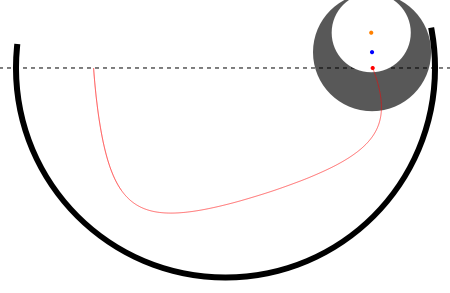
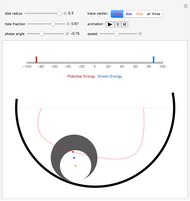
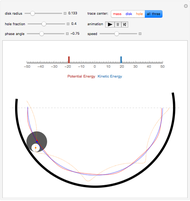
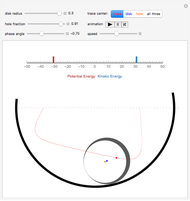
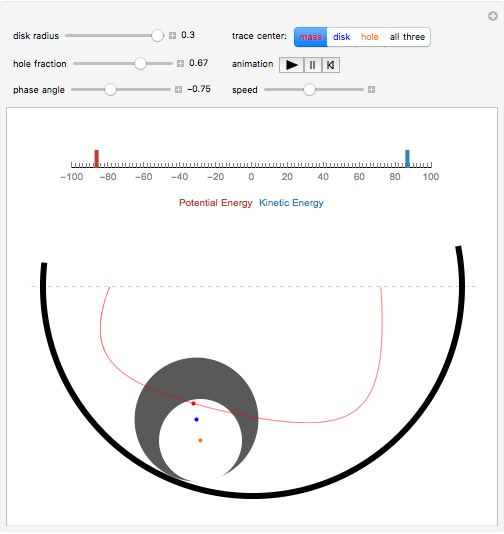
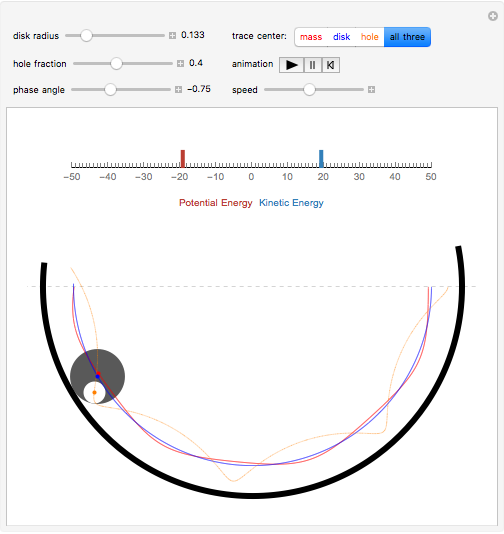
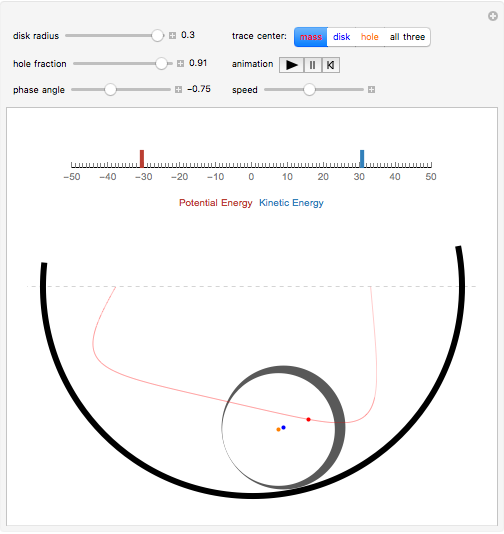
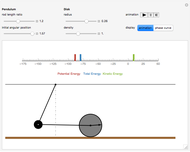
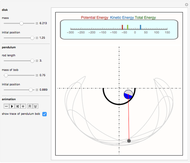
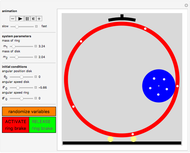
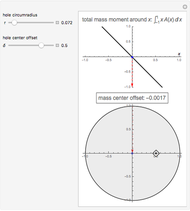
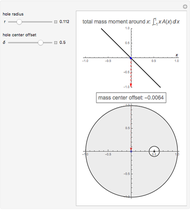
The center of mass of a disk with a hole is offset from the disk's geometric center, so that as the disk rolls in a circular well its motion is irregular.
[more]
Contributed by: Erik Mahieu (April 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Consider a disk of mass 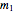 and radius
and radius 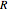 . The disk has a hole with radius
. The disk has a hole with radius  at a distance
at a distance  from its center. The mass cut out by the hole is
from its center. The mass cut out by the hole is 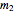 .
.
The potential energy of the disk plus hole is 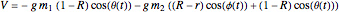 .
.
The kinetic energy of the system is 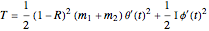 ,
where
,
where 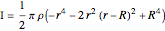 is the moment of inertia of the disk plus hole.
is the moment of inertia of the disk plus hole.
The Lagrangian 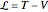 gives the equation of motion:
gives the equation of motion: 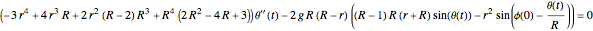 .
.
Permanent Citation