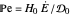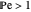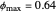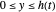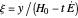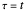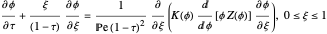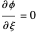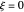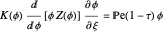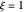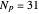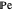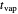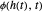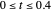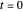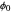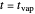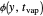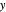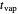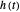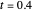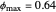Distribution of Colloidal Particles during Solvent Evaporation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
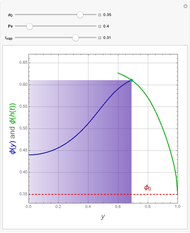
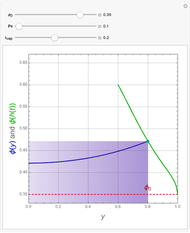
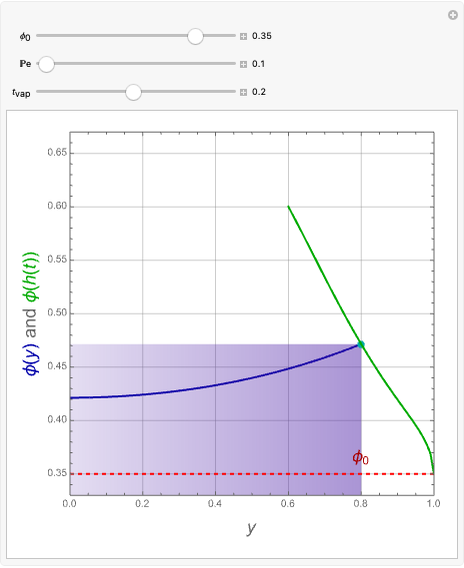
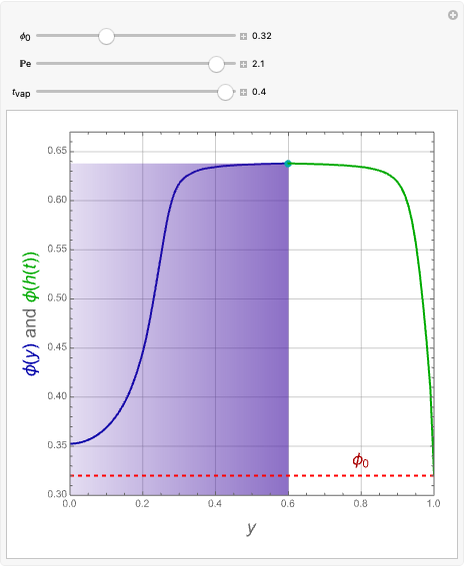
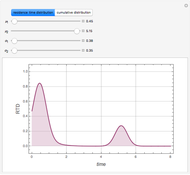
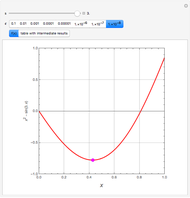
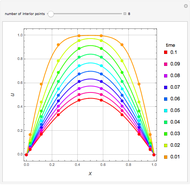
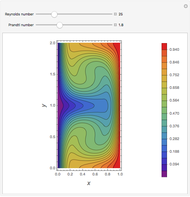
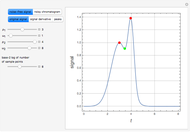
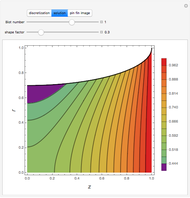
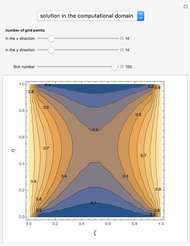
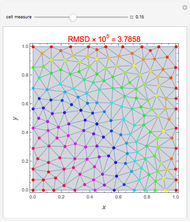
This Demonstration examines the underlying processes that take place when a colloidal dispersion of uniform thickness 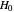 consolidates as solvent is removed. The overlying gas phase is assumed to be unsaturated with vapor, thereby providing the driving force for solvent evaporation to take place. The evaporation rate can be expressed as
consolidates as solvent is removed. The overlying gas phase is assumed to be unsaturated with vapor, thereby providing the driving force for solvent evaporation to take place. The evaporation rate can be expressed as 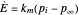 , where
, where 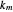 is an appropriate mass transfer coefficient and
is an appropriate mass transfer coefficient and 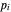 and
and 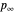 are the vapor pressures at the interface and in the bulk air, respectively. As the solvent evaporates (
are the vapor pressures at the interface and in the bulk air, respectively. As the solvent evaporates (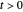 ), the film thins and particles begin to consolidate at the gas–liquid interface
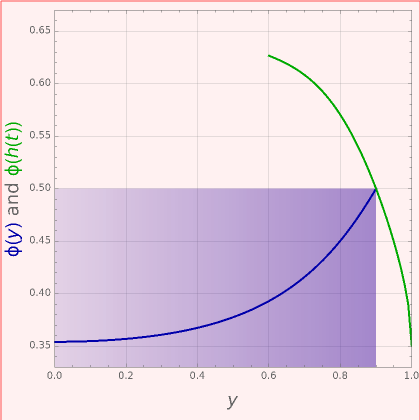
), the film thins and particles begin to consolidate at the gas–liquid interface 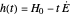 . The distribution of particles at any instant in time is denoted by
. The distribution of particles at any instant in time is denoted by 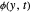 .
.
Contributed by: Brian G. Higgins and Housam Binous (September 2016)
Open content licensed under CC BY-NC-SA
Details
Reference
[1] A. F. Routh and W. B. Zimmerman, "Distribution of Particles during Solvent Evaporation from Films," Chemical Engineering Science, 59(14), 2004 pp. 2961–2968. doi:10.1016/j.ces.2004.04.027.
Snapshots
Permanent Citation