Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Dynamics of a Chain of Coupled Pendulums

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

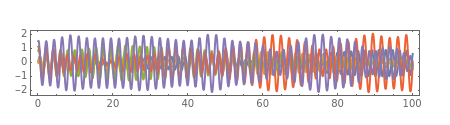
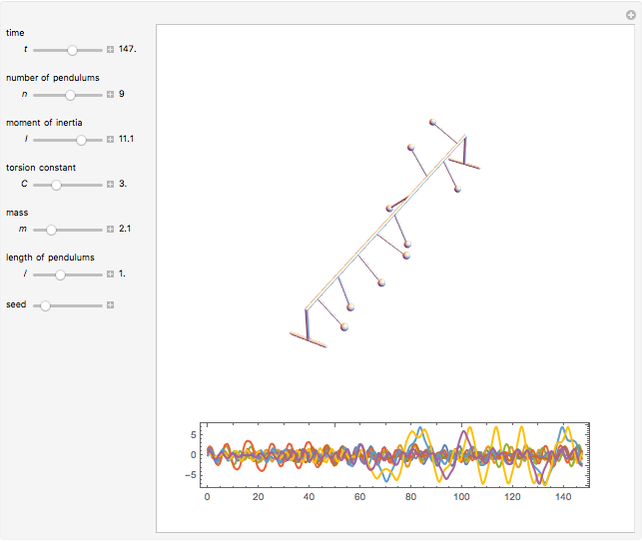
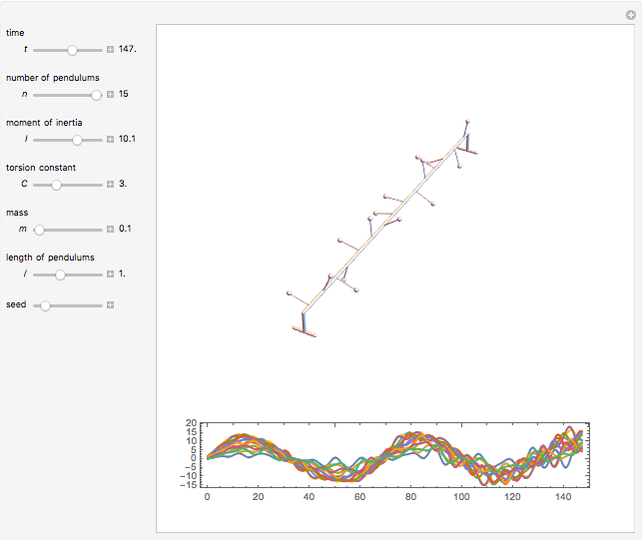
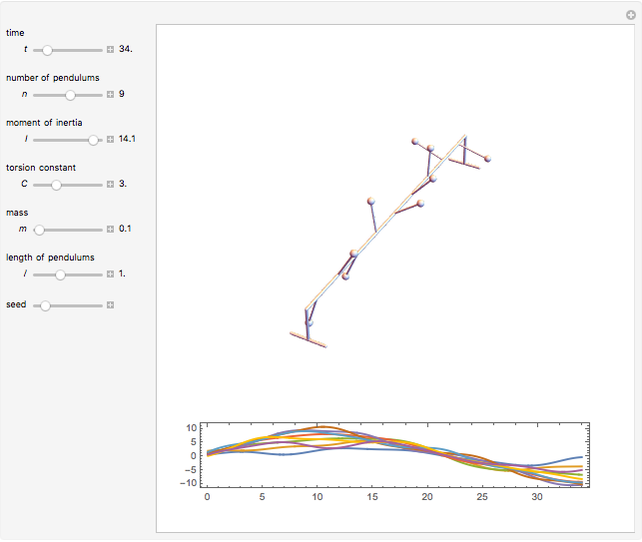
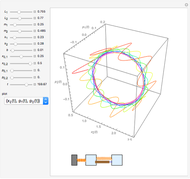
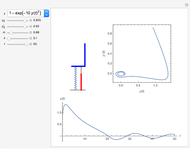
A row of pendulums coupled by torsion springs hangs from a common axis. In the continuum limit, the corresponding system of nonlinear differential equations approaches the sine-Gordon equation, whose solutions can exhibit solitons.

Contributed by: Enrique Zeleny (April 2013)
Open content licensed under CC BY-NC-SA

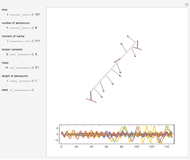
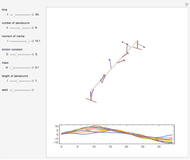
Snapshots

Details

The system of nonlinear coupled differential equations derived from the Hamiltonian is

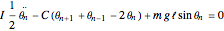, where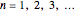

and 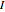is the moment of inertia, 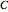is a torsion constant, 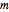is the mass, is the gravitational acceleration, and 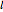is the length of the pendulums.

Reference

[1] T. Dauxois, M. Peyrard, Physics of Solitons, New York: Cambridge University Press, 2006 pp. 42–44.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send