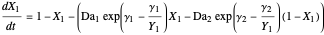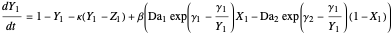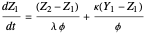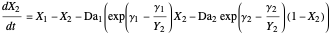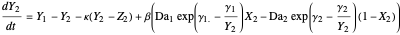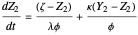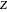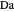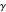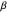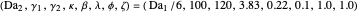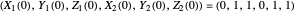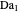Dynamics of Counter-Current Cooled CSTRs
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
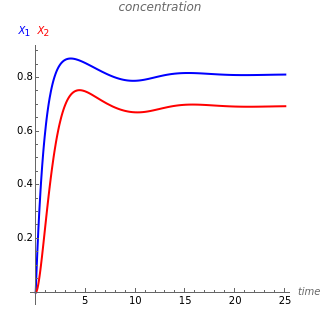
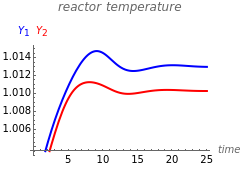
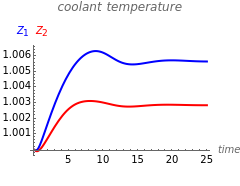
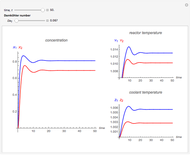
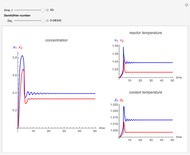
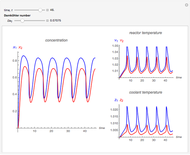
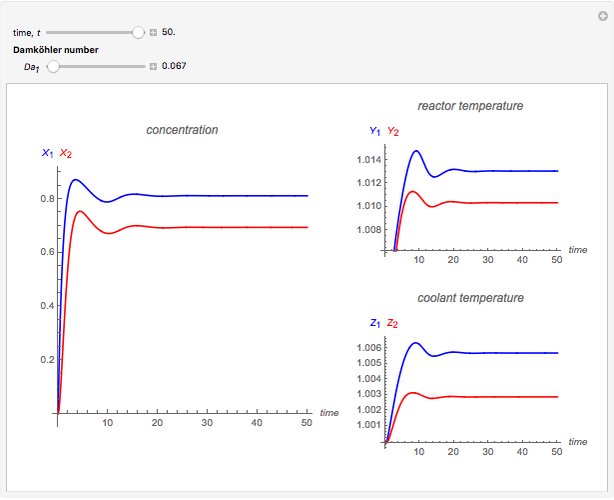
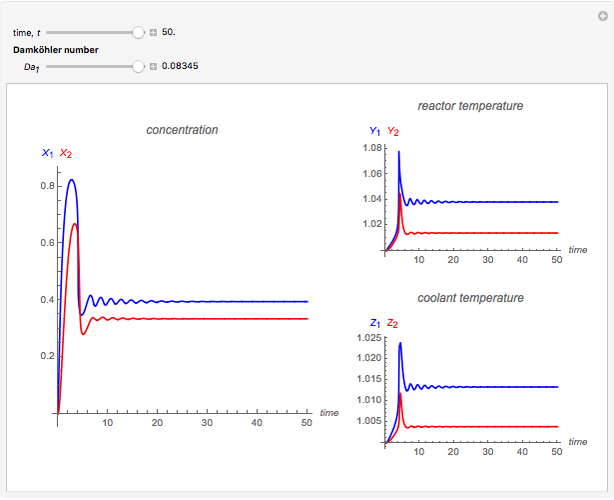
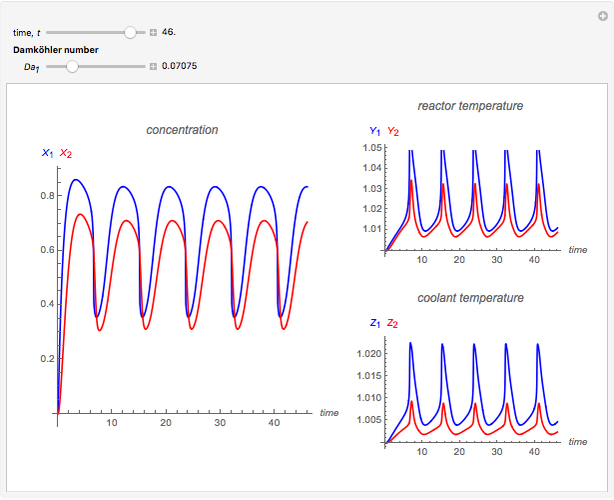
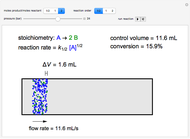
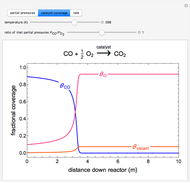
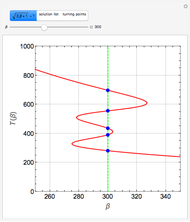
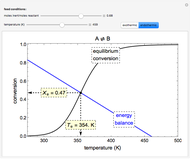
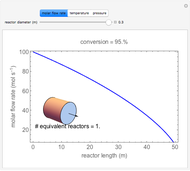
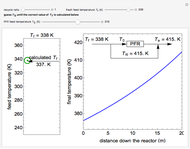
This Demonstration illustrates the dynamics of a system composed of two CSTRs in series with counter-current cooling in which a first-order reversible exothermic chemical reaction 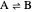 takes place. The system of two identical CSTRs is governed by six dimensionless differential equations [1]:
takes place. The system of two identical CSTRs is governed by six dimensionless differential equations [1]:
Contributed by: Clay Gruesbeck (September 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] K. S. Chang and R. Aris, "Chaotic Dynamics of Counter Currently Cooled CSTRs," Latin American Applied Research, 18, 1988 pp. 1–30.
Permanent Citation