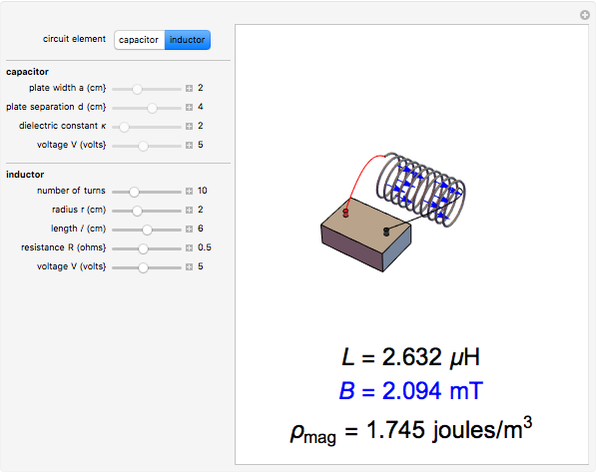
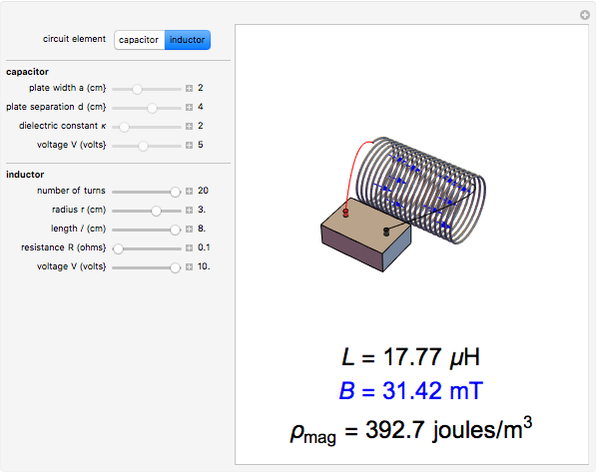
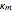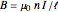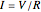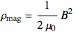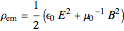Electromagnetic Field Energies in Capacitors and Inductors

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
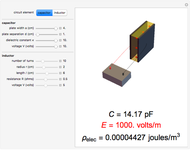
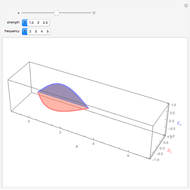
A capacitor with square plates of width  separated by a distance
separated by a distance  with a filler of dielectric constant (relative permittivity)
with a filler of dielectric constant (relative permittivity)  has a capacitance given by
has a capacitance given by 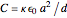 . Typical values are in the range of picofarads (pF). A voltage
. Typical values are in the range of picofarads (pF). A voltage  can hold positive and negative charges
can hold positive and negative charges 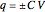 on the plates of the capacitor while producing an internal electric field
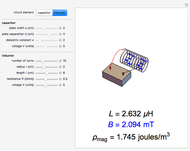
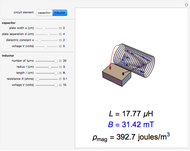
on the plates of the capacitor while producing an internal electric field 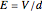 . Assuming idealized geometry, the energy of a charged capacitor equals
. Assuming idealized geometry, the energy of a charged capacitor equals 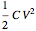 . This energy can be considered to be stored in the electric field, which implies a corresponding energy density
. This energy can be considered to be stored in the electric field, which implies a corresponding energy density 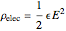 (with
(with 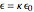 ).
).
Contributed by: S. M. Blinder (May 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation