Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Electron Conductance Models Using Maximal Entropy Random Walks

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

We use thermodynamic models for systems for which we have incomplete information. These models are based on theorems such as the maximum uncertainty principle, which states that we should choose the scenario which maximizes the entropy of the statistical ensemble.

[more]

To model the behavior of particles plotted on a lattice, we usually use simplified models, which maximize the entropy locally: for each vertex, assume uniform probability among the possible outgoing edges: generic random walk (GRW). By considering a lattice with defects and adding a potential gradient, we can simulate classical electron conductance models.

Recently introduced models maximize entropy among possible stochastic processes, assuming a uniform distribution among possible paths: maximal entropy random walk (MERW). This leads to completely different stationary probabilistic densities, just as for the corresponding quantum ground state. This is expected also from quantum statistical thermodynamics and should give better approximations for nanoscale current flow.

This Demonstration enables you to compare stationary and dynamical behavior for both models in 2D, for various defect densities and potential gradients.

[less]

Contributed by: Jarek Duda (August 2016)
Open content licensed under CC BY-NC-SA

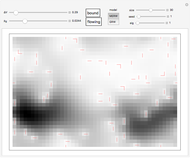
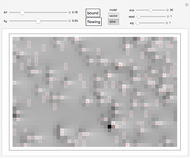
Snapshots

Details

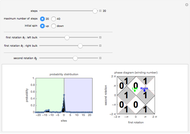
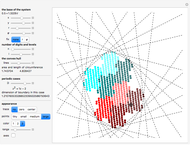
To emphasize some scenarios in thermodynamical models, we fix the energy instead of assuming a uniform probability distribution. The Boltzmann distribution is a compromise between maximizing entropy and minimizing energy.

We can use the Boltzmann distribution in two different ways: locally, for each vertex of the outgoing edges (natural expansion of GRW); or globally, considering entire paths (MERW analog).

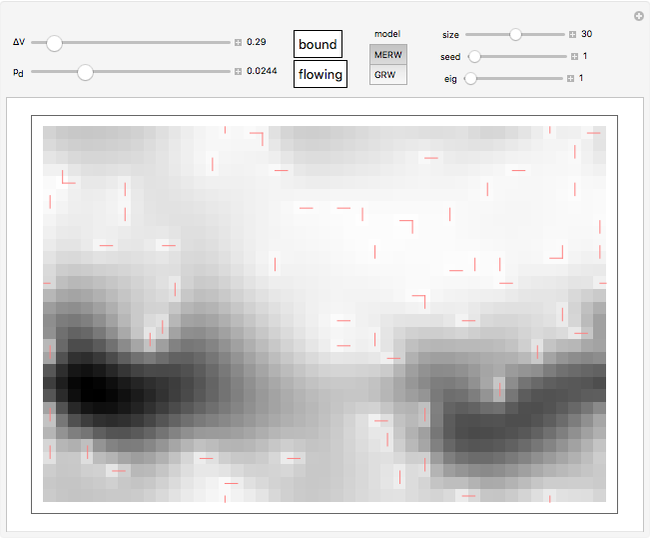
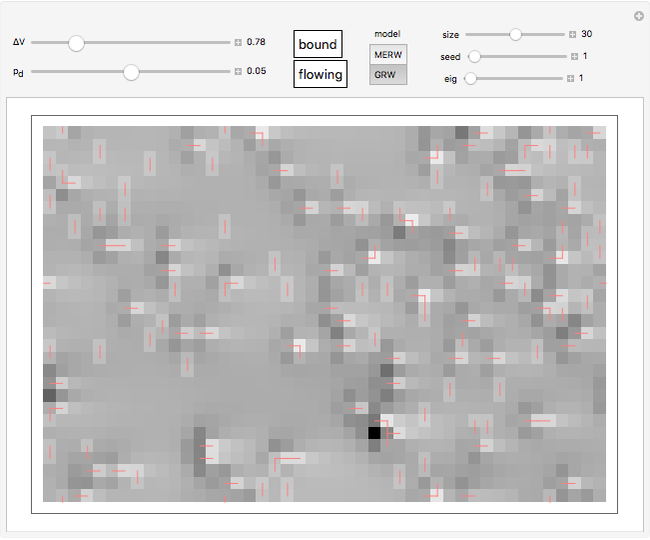
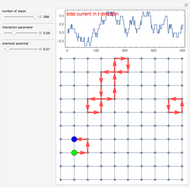
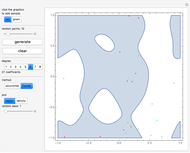
The controls let you choose the potential gradient 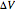, the edge removal probability from the regular 2D lattice 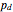, the size of the lattice and the number of a pseudorandom "seed". The "bound" button lets you toggle the cyclical boundary conditions in the vertical direction. The "eig" slider lets you use some other eigenvector than the dominant one.

The "flowing" button lets you switch between stationary probability density and dynamic current flow. By clicking the graphic you can choose the point at which the current is injected.

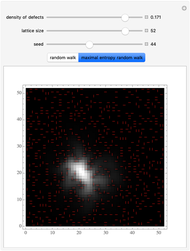
For more information about localization properties in quantum mechanics observed in a random walk see [1].

More information about the extended models and their relation to quantum mechanics can be found in [2].

References

[1] Z. Burda, J. Duda, J. M. Luck and B. Waclaw, "Localization of the Maximal Entropy Random Walk," Physical Review Letters, 102(16), 2009 160602. doi:10.1103/PhysRevLett.102.160602.

[2] J. Duda, "From Maximal Entropy Random Walk to Quantum Thermodynamics." arxiv.org/abs/1111.2253.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send