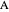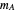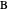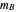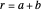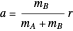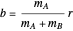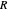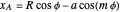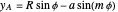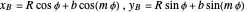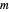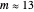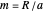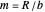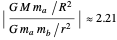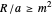Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Epicycles Revisited; Convexity of Lunar Orbit about the Sun

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

Kepler's laws of planetary motion in the 17th century superseded the Ptolemaic system of epicycles to account for the detailed motions of the planets. Generalizations of epicycloids, called epitroichoids, still do occur, however, in the description of relative planet-moon motions as their barycenters (centers of gravity) follow Keplerian orbits around the Sun.

[more]

We consider a simplified idealized case, which is justified in the Details: a moon (red point ) with mass is in a circular orbit about its planet (blue point ) with mass , with the moon-planet distance equal to , where and are the respective distances of the moon and planet from their barycenter. The barycenter of this pair is in a circular orbit of radius about the Sun. With the Sun at the origin, the parametric equations for and can be written

, ,

,

where equals the number of lunar cycles per revolution about the Sun. (For the Sun-Earth-Moon system, .) These represent parametric equations for epitroichoids, which reduce to the more familiar epicycloids when and in the first and second set of equations, respectively. In most cases these curves exhibit a looped or cuspoid structure as they traverse the larger circle. All rotations and revolutions shown are counterclockwise.

This brings us to the remarkable fact that the Moon's orbit around the Sun is a convex curve. This can be explained by the following physical argument. The gravitational force of the Sun on the Moon is always more than twice the gravitational force of the Earth on the Moon: . Thus the net force on the Moon is always directed toward the Sun. But, by Newton's second law, this force is proportional to the second derivative of with respect to time, hence the radial curvature of the orbit is always positive. This implies that the Moon’s orbit is always convex with respect to the Sun. In terms of the epitrochoid parameters, the condition for convexity can be expressed as , which is easily fulfilled for the Sun and Moon. Remarkably, no other known planet-moon couple in the Solar System obeys the convexity condition.

[less]

Contributed by: S. M. Blinder (May 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The three-body Sun-Earth-Moon problem can be described by the Lagrangian

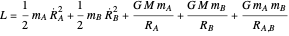
where the Sun is taken as the origin of the coordinate system and is thus considered stationary. Here 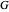represents the gravitational constant, 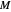the solar mass, 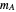the lunar (or other moon) mass, 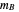the Earth (or other planetary mass), and 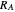, , 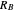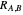the three interbody distances. Because of the great disparity in masses and in distances, an accurate simplification of the problem is possible. For the Sun-Earth-Moon system, 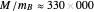, , 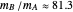and 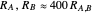. The Lagrangian is well approximated by

]

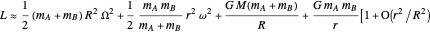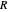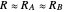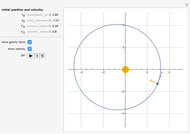
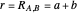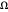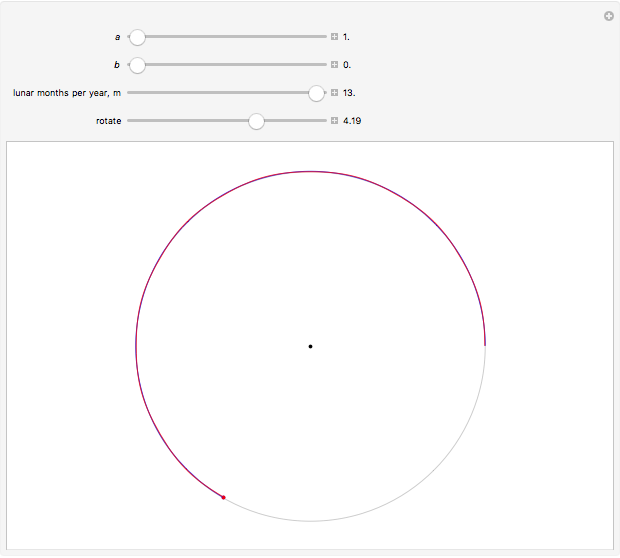
where is the distance from the Sun to the Earth-Moon barycenter () and . The simplest case is when both orbital motions are circular, with angular velocities ("annual") and 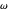("monthly"). To a fair approximation, there are 13 lunar months per solar year: .

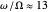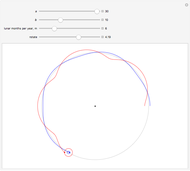
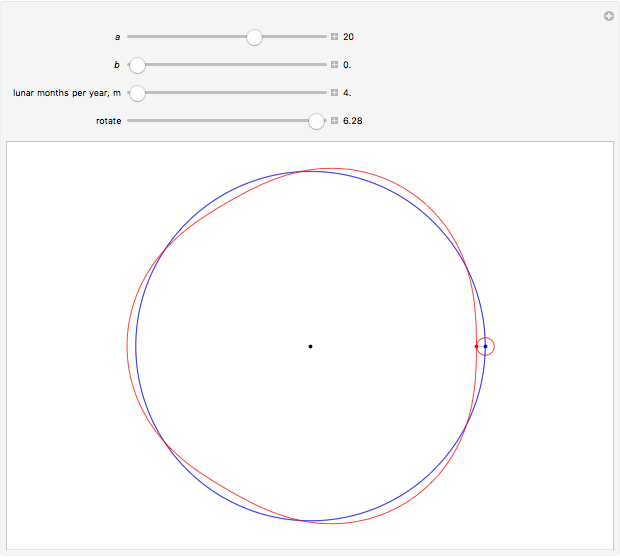
The thumbnail graphic for this Demonstration shows epichoroidal orbits for a hypothetical twin planet around some other star, in which a planet and its moon are of equal mass.

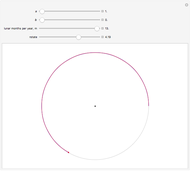
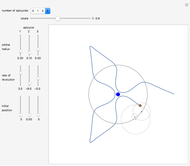
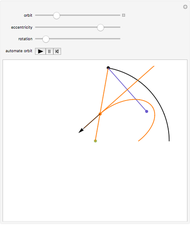
Snapshot 1: a qualitative representation for a planet with a very massive moon; for example Pluto's moon Charon has approximately 11.6% of the mass of the planet

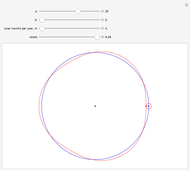
Snapshot 2: the Sun-Earth-Moon system drawn to scale, with 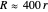(average Sun-Earth distance is about 400 times average Earth-Moon distance) and 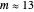(lunar months per year); with higher magnification, it can be seen that the Moon's orbit around the Sun is a distorted 13-sided polygon that is a convex figure

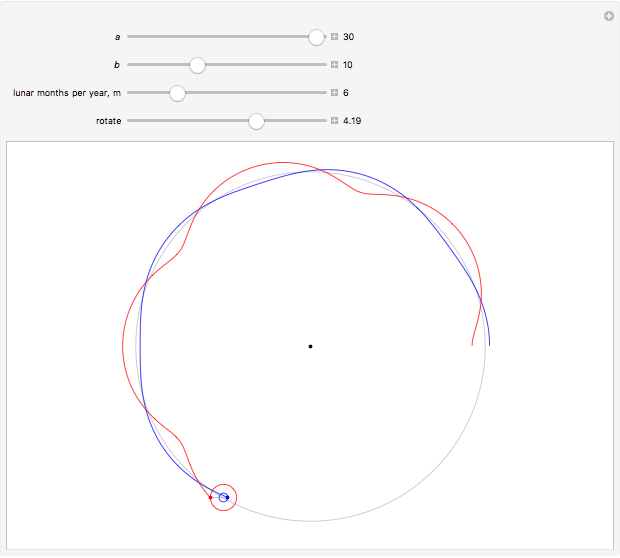
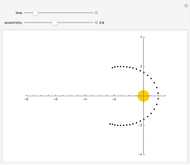
Snapshot 3: a toy model of the Sun-Earth-Moon system, with 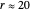and 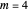, in which the requisite inequality for convexity is fulfilled and much easier to verify

References

[1] N. S. Brannen, "The Sun, the Moon, and Convexity," The College Mathematics Journal, 32(4), 2001 pp. 268–272.

[2] L. Hodges, "Why the Moon's Orbit is Convex," The College Mathematics Journal, 33(2), 2002 pp. 169–170.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send