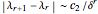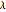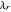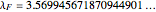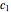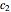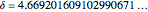Feigenbaum's Scaling Law for the Logistic Map

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
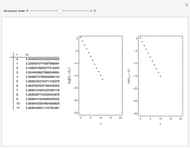
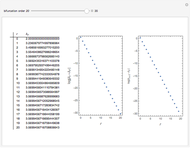
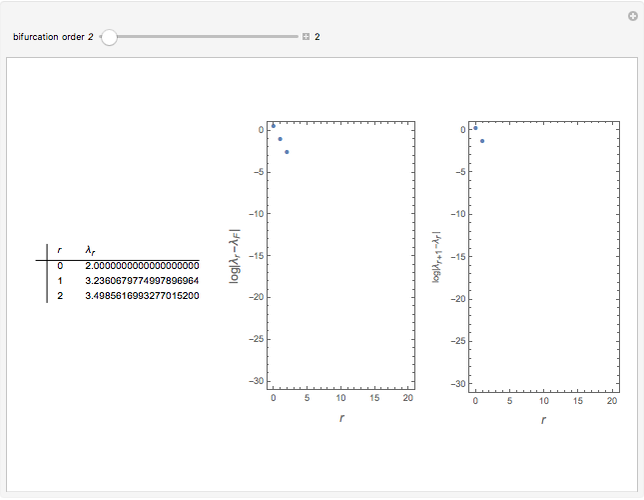
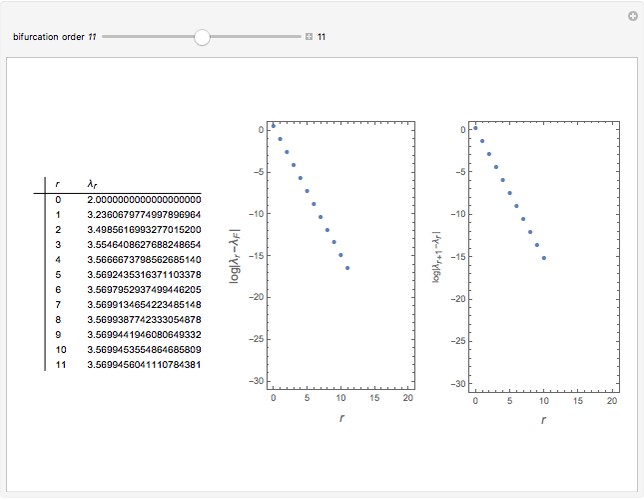
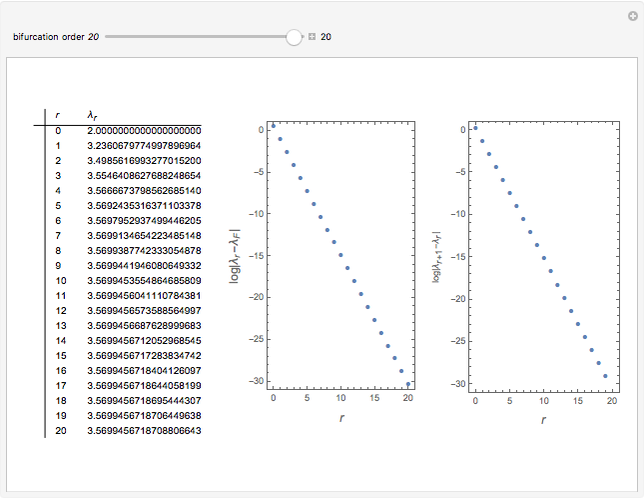
Mitchell Feigenbaum's one-term parameter scaling laws for the logistic map are
[more]
Contributed by: Ki-Jung Moon (October 2013)
Open content licensed under CC BY-NC-SA
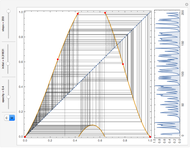
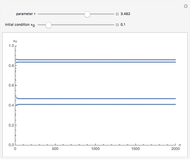
Snapshots
Details
More information on Feigenbaum's one-term parameter scaling laws can be found in [1–4].
References
[1] M. J. Feigenbaum, "Quantitative Universality for a Class of Non-Linear Transformations," Journal of Statistical Physics, 19, 1978 pp. 25–52.
[2] M. J. Feigenbaum, "The Universal Metric Properties of Nonlinear Transformations," Journal of Statistical Physics, 21, 1979 pp. 669–706.
[3] K.-J. Moon, "Reducible Expansions and Related Sharp Crossovers in Feigenbaum's Renormalization Field," Chaos: An Interdisciplinary Journal of Nonlinear Science, 18, 2008, 023104.
[4] K.-J. Moon, "Erratum: Reducible Expansions and Related Sharp Crossovers in Feigenbaum's Renormalization Field," Chaos: An Interdisciplinary Journal of Nonlinear Science, 20, 2010, 049902.
Permanent Citation