Fifteen Great Circles on a Sphere

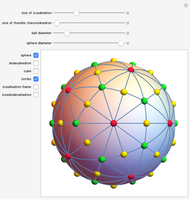
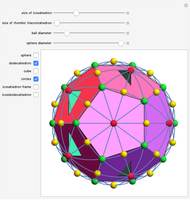
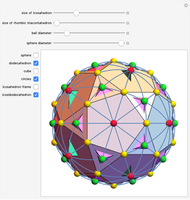
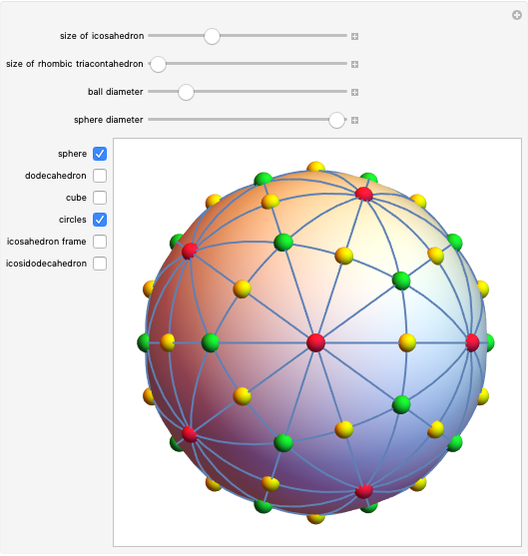
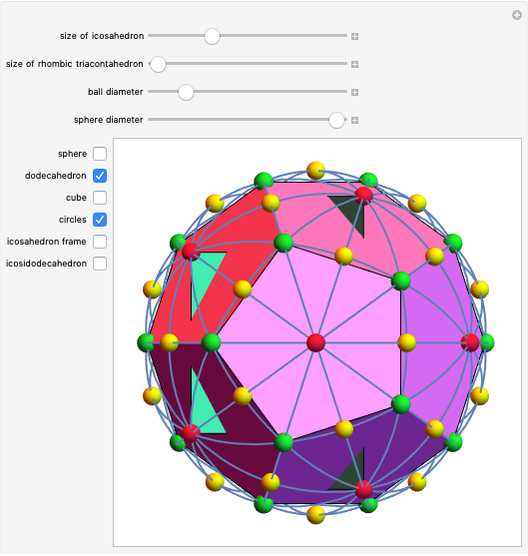
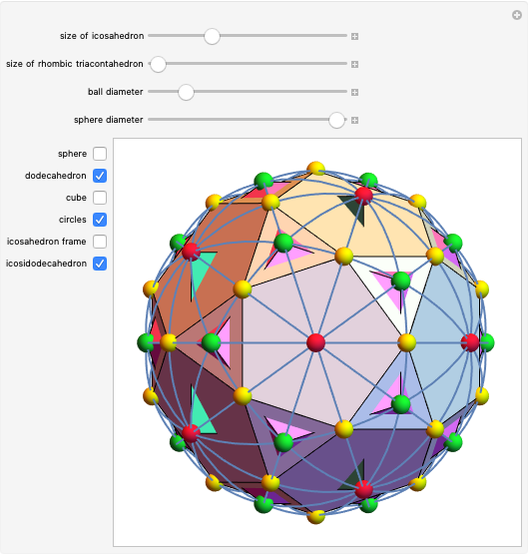
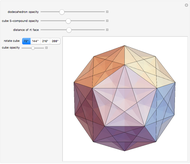
Three golden rectangles at right angles to each other determine the vertices of an icosahedron. There are 15 different circles through the pairs of opposite edges of the icosahedron. These circles are the great circles of a sphere circumscribing the icosahedron, since they are in the plane of the golden rectangles, and by one definition, a great circle is the intersection of a sphere and a plane passing through the center of the sphere. The intersections of the circles determine the vertices of a dodecahedron and an icosidodecahedron. The 30 edges of the icosahedron coincide with the longer diagonals of the golden rhombus bordering the rhombic triacontahedron.