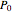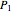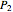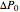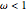Focus and Directrix in a Quadratic Bézier Curve
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
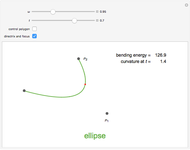
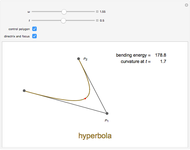
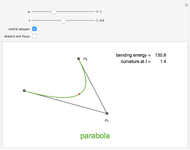
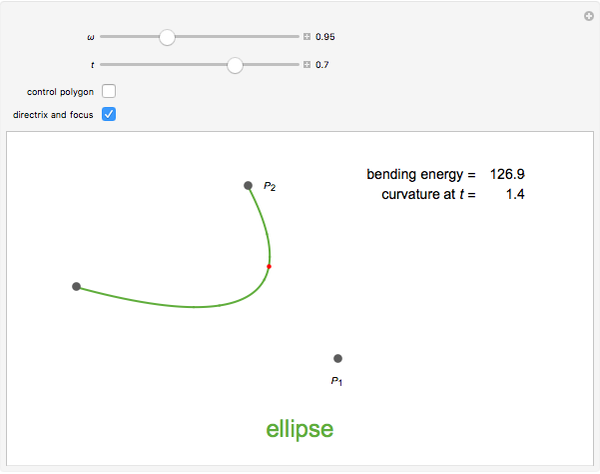
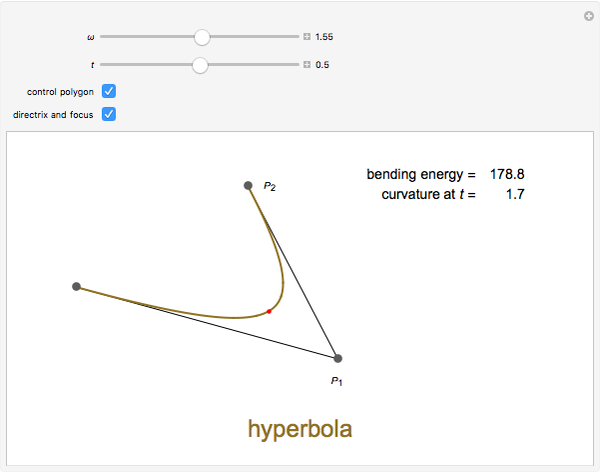
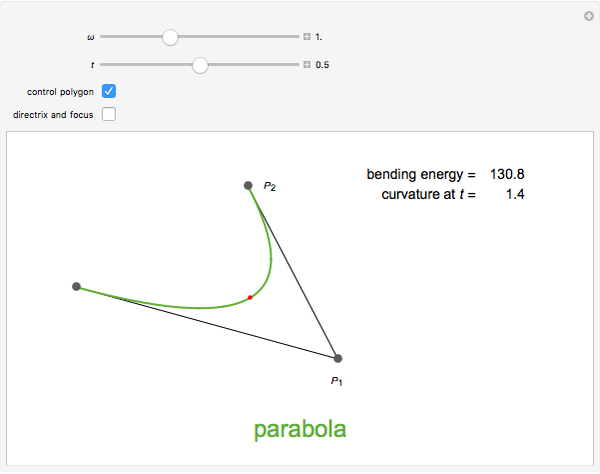
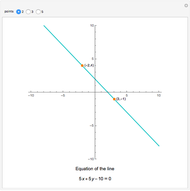
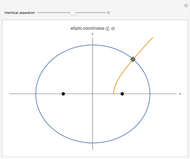
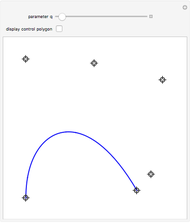
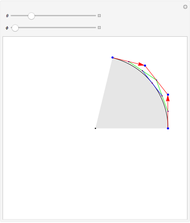
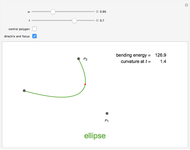
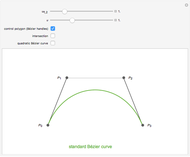
Any quadratic Bézier curve (with unit parameter  ) represents a parabolic segment. This Demonstration illustrates the relationship between the disposition of the points and the vertex, locus, and directrix of the corresponding parabola.
) represents a parabolic segment. This Demonstration illustrates the relationship between the disposition of the points and the vertex, locus, and directrix of the corresponding parabola.
Contributed by: Alexis Luengas Zimmer (October 2012)
Based on a program by: Isabelle Cattiaux-Huillard and Gudrun Albrecht
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation