Geodesics in Schwarzschild Space

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
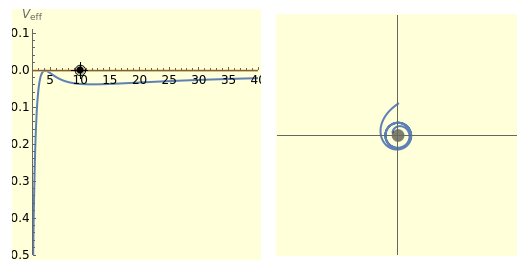
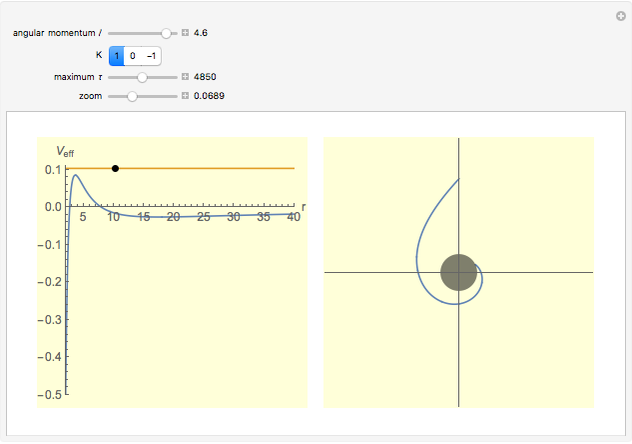
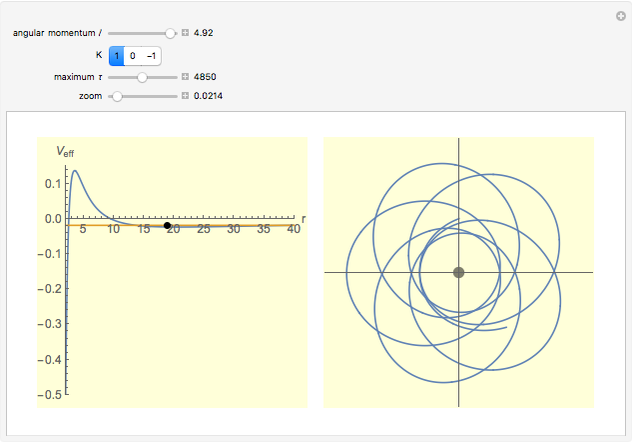
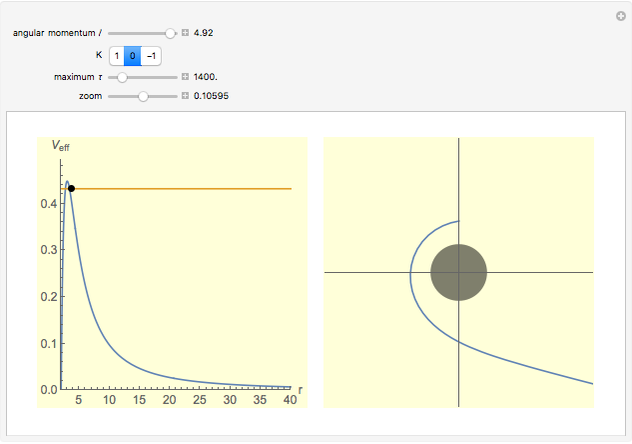
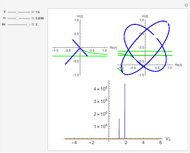
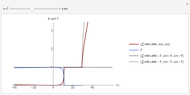
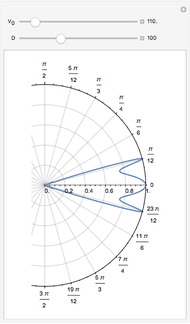
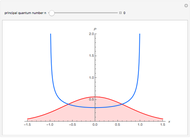
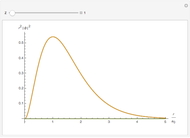
The right-hand side of the graphic in this Demonstration shows a geodesic outside the Schwarzschild radius 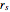 , while the left-hand side shows the effective radial potential. The latter depends on the value of the angular momentum
, while the left-hand side shows the effective radial potential. The latter depends on the value of the angular momentum  , which you can vary with the first slider. The effective radial potential also depends on
, which you can vary with the first slider. The effective radial potential also depends on 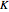 : a particle orbit has
: a particle orbit has 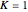 , a null geodesic (such as a light-ray) has
, a null geodesic (such as a light-ray) has 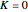 , and a time-like geodesic has
, and a time-like geodesic has  . You can specify the starting point of the integration for both energy and radius by clicking on an allowed value, on or above the curve on the left.
. You can specify the starting point of the integration for both energy and radius by clicking on an allowed value, on or above the curve on the left.
Contributed by: Niels Walet (December 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The right-hand pane in this Demonstration shows a geodesic outside the Schwarzschild radius 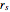 , assuming a spherical mass distribution or point mass of total mass
, assuming a spherical mass distribution or point mass of total mass 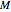 inside this radius. This would include the case of a black hole. On the left, we show the effective radial potential. As discussed in some detail in standard textbooks (e.g., [1]), this depends on the value of the angular momentum
inside this radius. This would include the case of a black hole. On the left, we show the effective radial potential. As discussed in some detail in standard textbooks (e.g., [1]), this depends on the value of the angular momentum  . It also depends on whether we are looking at a particle orbit (
. It also depends on whether we are looking at a particle orbit (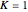 ), a null geodesic (say, a light-ray,
), a null geodesic (say, a light-ray, 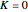 ) or a time-like geodesic (
) or a time-like geodesic ( ).
).
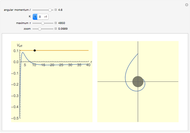
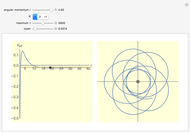
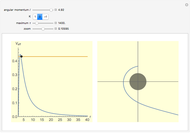
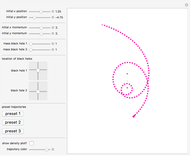
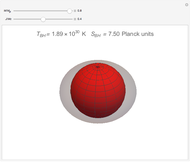
The snapshots show a couple of interesting cases. The first one shows a "plunge orbit", in which a particle falls into the singularity at the origin; the second shows a precessing bound-state orbit, notably different from the classical Keplerian case. The third shows that near the maximum of the potential, light evolves into an almost bound state orbit (there is an unstable bound state at the top). The final picture shows a time-like geodesic, which closely resembles the behavior of a light ray.
This work was influenced by David Saroff's Demonstration on black-hole orbits [2].
References
[1] J. B. Hartle, Gravity: An Introduction to Einstein's General Relativity, San Francisco, CA: Addison-Wesley, 2003.
[2] D. Saroff. "Orbits around Schwarzschild Black Holes" from the Wolfram Demonstrations Project—A Wolfram Web Resource. www.demonstrations.wolfram.com/OrbitsAroundSchwarzschildBlackHoles.
Permanent Citation