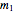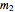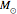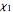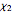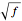Gravitational Waves from Non-precessing Spinning Binary Black Hole Coalescence

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
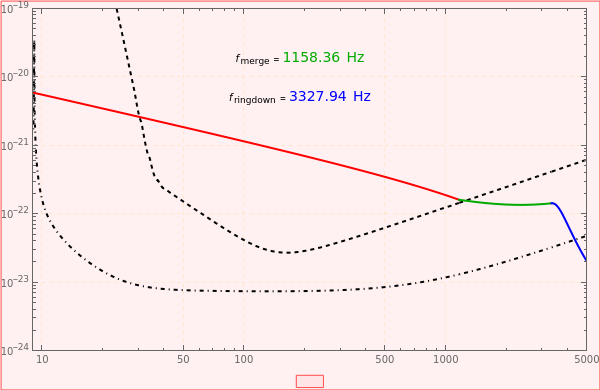
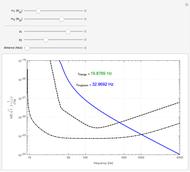
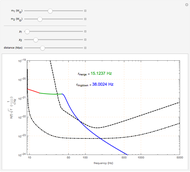
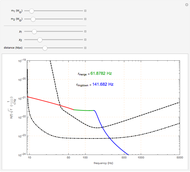
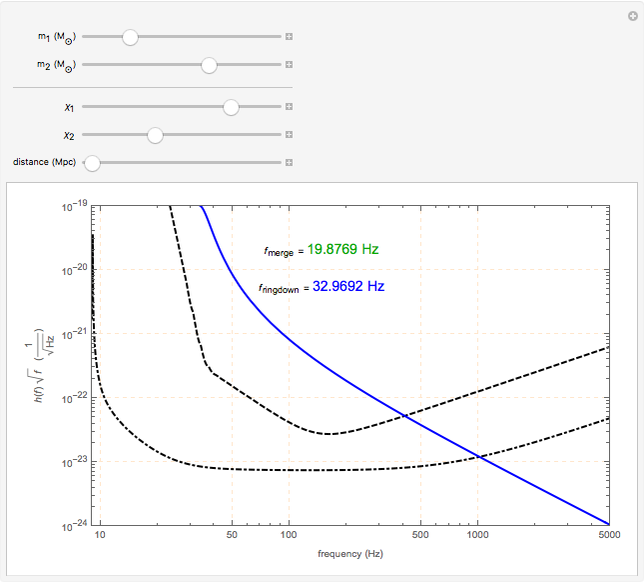
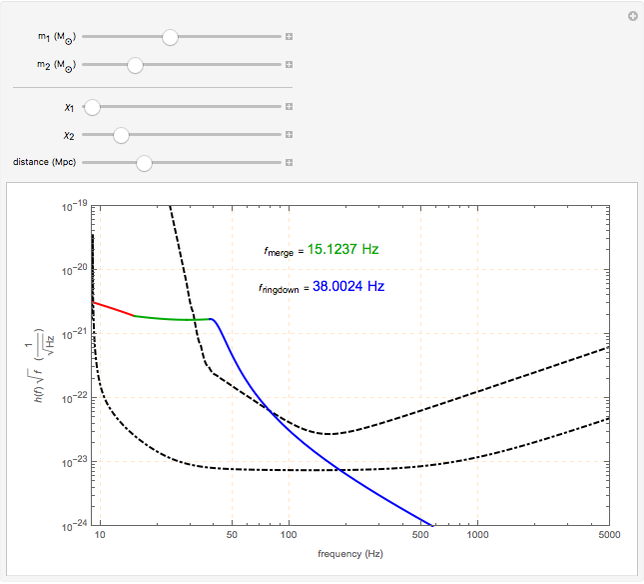
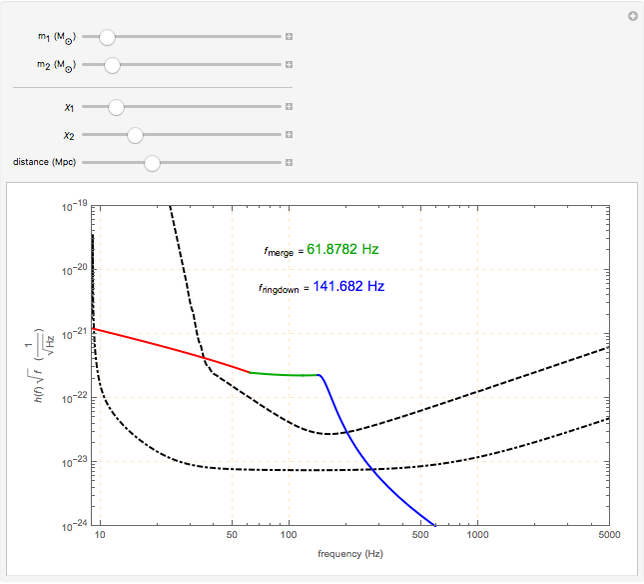
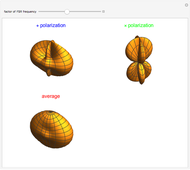
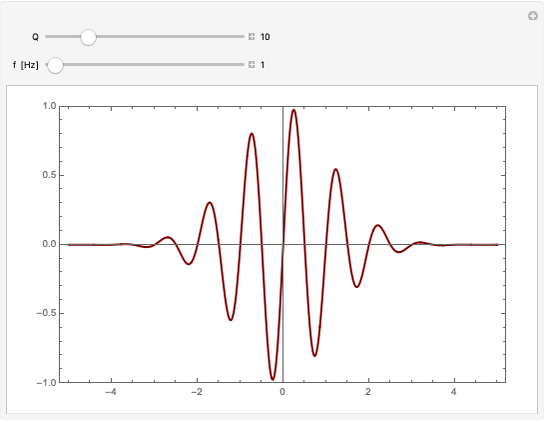
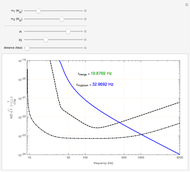
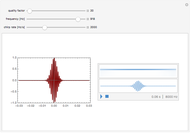
This Demonstration shows the Fourier amplitude of the gravitational wave from the coalescence of two non-precessing spinning black holes. The inspiral region is shown in red, the merger is shown in green, and the ringdown is shown in blue. The amplitude spectral density (ASD) for initial Laser Interferometer Gravitational-Wave Observatory (LIGO) design is shown as a dashed line. The ASD for advanced LIGO is shown as a dot-dashed line.
[more]
Contributed by: Satya Mohapatra (March 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The coalescence of a binary black hole has three phases. When the two black holes are far from each other, the phase is known as inspiral. The gravitational wave from this phase has the leading-order dependence of 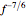 as a function of frequency. A gravitational wave is emitted in the merger phase when the two black holes come close to each other and are about to merge. In the merger phase, the gravitational wave has the leading-order frequency dependency
as a function of frequency. A gravitational wave is emitted in the merger phase when the two black holes come close to each other and are about to merge. In the merger phase, the gravitational wave has the leading-order frequency dependency 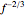 . The two black holes merge to form a single Kerr black hole. Just after the merger, the resulting black hole is still in an excited stage. It emits quasinormal ringdown radiation. The ringdown is modeled as a one-sided Lorentzian function in the frequency domain. The merger phase begins at the frequency
. The two black holes merge to form a single Kerr black hole. Just after the merger, the resulting black hole is still in an excited stage. It emits quasinormal ringdown radiation. The ringdown is modeled as a one-sided Lorentzian function in the frequency domain. The merger phase begins at the frequency 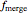 . The ringdown phase starts at the end of the merger phase, with an associated ringdown frequency
. The ringdown phase starts at the end of the merger phase, with an associated ringdown frequency  .
.
For a Kerr black hole to have an event horizon, it is necessary that 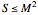 , where
, where 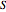 is the spin angular momentum and
is the spin angular momentum and 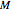 is the total mass of the system. Otherwise a naked singularity would result. The spin parameter is defined by the dimensionless parameter,
is the total mass of the system. Otherwise a naked singularity would result. The spin parameter is defined by the dimensionless parameter, 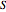 /
/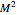 . For non-precessing spins, the spin of each black hole is directed either along the orbital angular momentum (positive value) or opposite to the orbital angular momentum (negative value). When the spins of the black holes are along the orbital angular momentum, their vector sum is the total angular momentum. When they are anti-parallel to the orbital angular momentum, they reduce the total angular momentum. Orbital hang-up is a very interesting phenomenon that occurs when the binary black hole system radiates out the extra angular momentum in a gravitational wave, so that it can form a stable Kerr black hole without a naked singularity. To radiate the extra angular momentum, the system remains in orbit for a longer time (hence the name hang-up), and this also results in an increase of the ringdown frequency.
. For non-precessing spins, the spin of each black hole is directed either along the orbital angular momentum (positive value) or opposite to the orbital angular momentum (negative value). When the spins of the black holes are along the orbital angular momentum, their vector sum is the total angular momentum. When they are anti-parallel to the orbital angular momentum, they reduce the total angular momentum. Orbital hang-up is a very interesting phenomenon that occurs when the binary black hole system radiates out the extra angular momentum in a gravitational wave, so that it can form a stable Kerr black hole without a naked singularity. To radiate the extra angular momentum, the system remains in orbit for a longer time (hence the name hang-up), and this also results in an increase of the ringdown frequency.
All the equations used in this Demonstration are given in [2]. For a catalog of hybridized non-precessing spinning binary black hole coalescence waveforms, see [3]. The sensitivities (amplitude spectral density) shown for initial LIGO and advanced LIGO are obtained from [4] and [5].
References
[1] LIGO Scientific Collaboration. "Introduction to LIGO and Gravitational Waves." (Apr 30, 2012) www.ligo.org/science.php.
[2] P. Ajith et al., "Inspiral-Merger-Ringdown Waveforms for Black-Hole Binaries with Non-precessing Spins," Physical Review Letters, 106(241101), 2011, Preprint: arXiv:gr-qc:0909.286.
[3] P. Ajith et al., "The NINJA-2 Catalog of Hybrid Post-Newtonian/Numerical-Relativity Waveforms for Non-Precessing Black-Hole Binaries," Preprint: arXiv:gr-qc: 1201.5319.
[4] LIGO. Initial LIGO science requirements. (Apr 30, 2012) www.ligo.caltech.edu/~lazz/distribution/LSC_Data/SRD_strain_ 4k.txt.
[5] LIGO. "LIGO DCC: T0900288: Advanced LIGO Anticipated Sensitivity Curves." (April 30, 2012) dcc.ligo.org/cgi-bin/DocDB/ShowDocument?docid=2974.
Permanent Citation