Wolfram Demonstrations Project

This Demonstration describes the dynamics of a pendulum made up of two springs. The top spring mass is taken into account in the dynamics, using Rayleigh's method of vibration analysis. The lower spring is assumed to be massless. The pendulum bob slides back and forth while attached to the end of the lower massless spring. The bob has three degrees of freedom. The equations of motion for the bob and the pendulum are derived using the Lagrangian method, and Mathematica's built-in function NDSolve is used to obtain a numerical solution.

Contributed by: Nasser M. Abbasi

Rotate and Zoom in 3D
Slider Zoom
Gamepad Controls
Automatic Animation

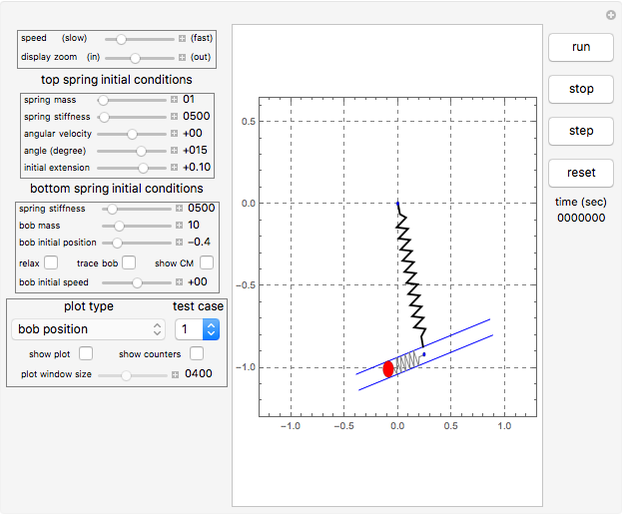
Description of the User Interface

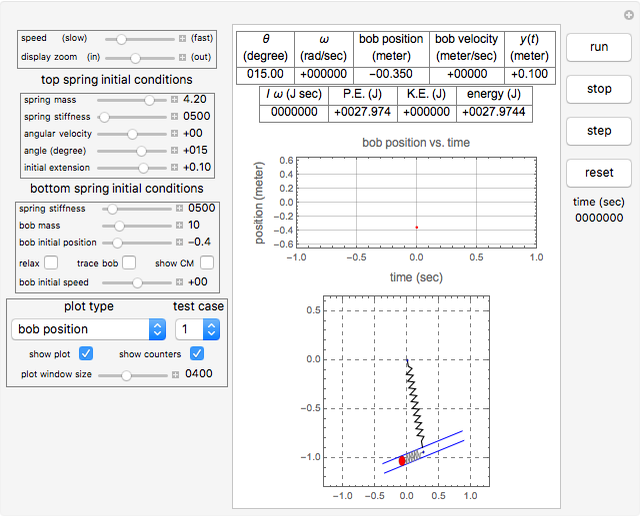
The four buttons on the right side are used to control the Demonstration. The "reset" button brings the Demonstration back to the initial conditions. There are two main sets of control variables. One is for setting the initial conditions for the top spring, and the second is for setting the initial conditions for the lower spring. The "relax" checkbox for the lower spring is used to put the spring into the relaxed position. For the top spring, the relaxed position is set at 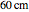60 cm, while the lower spring is assumed to have zero relaxed length located at the point where the two springs are joined. You can see a trace of the bob motion using the "trace" checkbox. You can see the location of the center of mass (CM) of the whole system using the "show CM" checkbox.

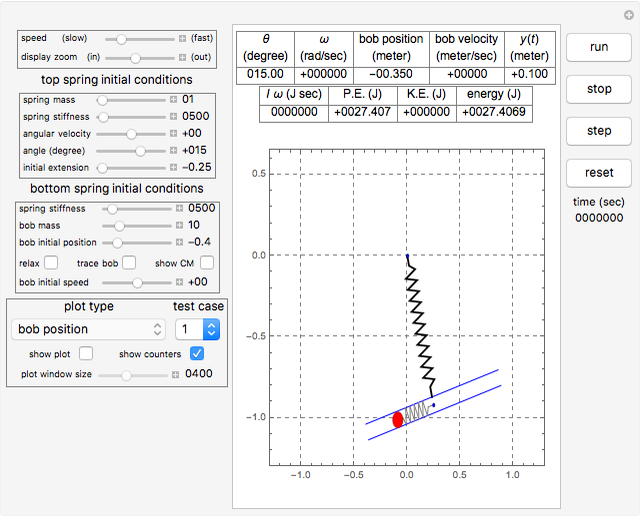
The result has three parts. The counters show the current state. The field labeled "energy" is the sum of the potential energy (P.E.) and the kinetic energy (K.E.). The field labeled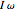

is the total angular momentum of the system. The field labeled

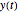is the current extension of the top spring measured from its relaxed position. You can see different plots by selecting the plot type using the popup menu labeled "plot type". The main display shows the pendulum itself as it swings.

A popup menu labeled "test case" is used to select one of three preconfigured parameters. Click the "run" button after selecting a test case to start the Demonstration.

The Demonstration runs with no throttling by using a single dynamic variable called "gTick" that is updated at the end of each Manipulate expression evaluation so that the Manipulate expression is reevaluated again immediately. This lets the Demonstration run at the maximum speed. A slider labeled "speed" can be used to adjust the speed of the Demonstration as needed.

The Demonstration runs continuously until you stop it. All units used are in SI.

Derivation of Equations of Motion

The equations of motion are derived using the Lagrangian procedure. Rayleigh's method is used for the top spring, such that the effective mass used is

of the top spring mass. This effective mass is added to the bob mass to account for the vertical displacement of the top spring. The bob has three degrees of freedom: the distance

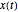along the length of the lower spring (

is the location where the top pendulum is attached to the lower pendulum), the angle of rotation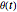

, and 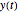the vertical displacement of the top spring

. For more information on the derivation of the equations of motion, see the author's report.

References

[1] D. Morin, Introduction to Classical Mechanics: With Problems and Solutions, New York: Cambridge University Press, 2008.

[3] Research & Education Association, REA's Problem Solvers: Mechanics: Statics and Dynamics, Piscataway, NJ: Research & Education Association, 2002.

[3] D. A. Wells, Schaum's Outline of Lagrangian Dynamics, New York: McGraw-Hill, 1967.

[2] S. Timoshenko, Vibration Problems in Engineering, 2nd ed., New York: D. Van. Nostrand, 1937.

[5] Wikipedia. "Effective Mass (Spring-Mass System)." (Sep 13, 2012) en.wikipedia.org/wiki/Effective_mass_ %28 spring-mass_system %29.