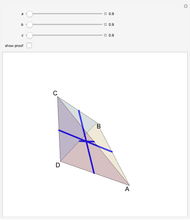
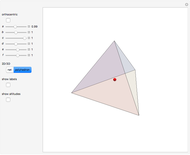
Heppes's Two-Tip Tetrahedron

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
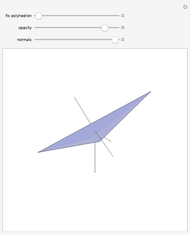
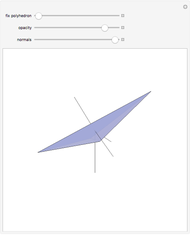
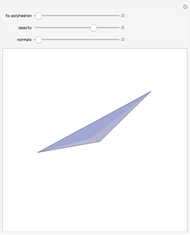
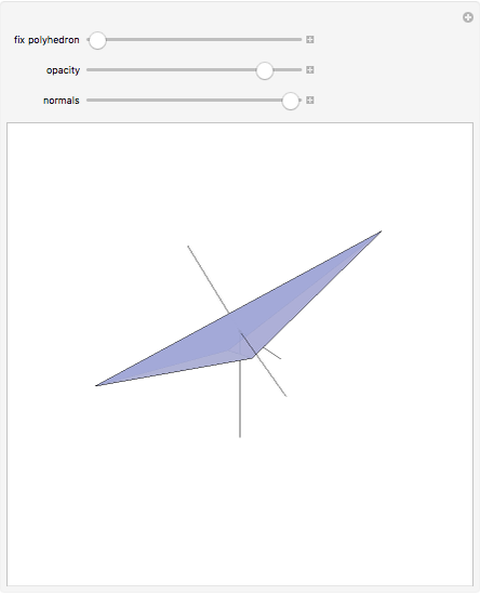
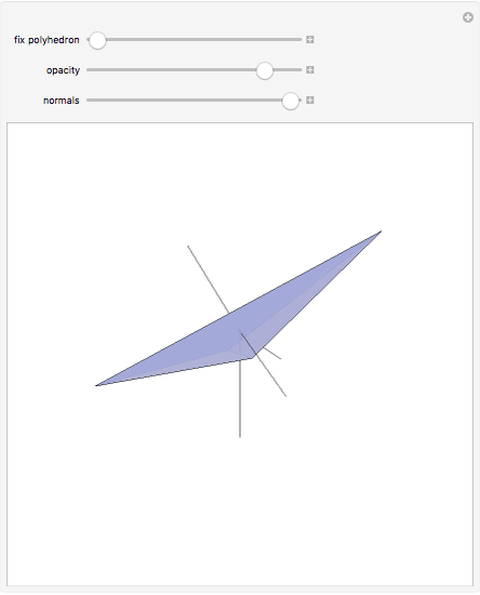
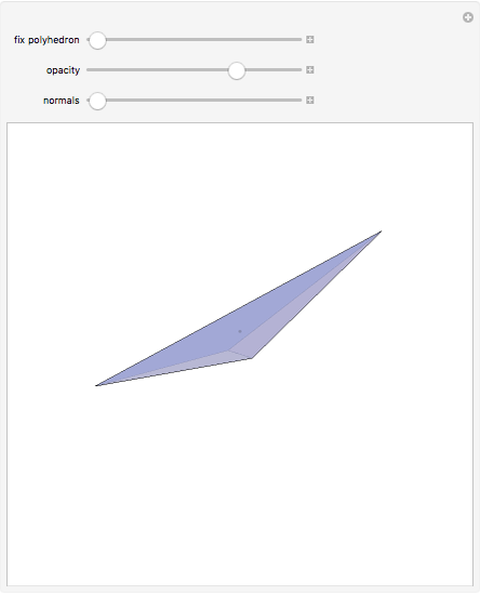
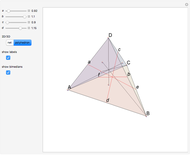
A face of a polyhedron is stable if and only if the orthogonal projection of the center of mass of the polyhedron onto the plane of the face lies inside the face or on an edge. In other words, when the polyhedron is placed on that face, the center of mass is over the face. This tetrahedron has two unstable faces. If you place it on one of the unstable faces, it will topple to the other unstable face and then topple to one of the stable faces.
Contributed by: Izidor Hafner (December 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] J. Bryant and C. Sangwin, How Round Is Your Circle?: Where Engineering and Mathematics Meet, Princeton, NJ: Princeton University Press, 2008, pp. 273–274.
Permanent Citation
"Heppes's Two-Tip Tetrahedron"
http://demonstrations.wolfram.com/HeppessTwoTipTetrahedron/
Wolfram Demonstrations Project
Published: December 3 2012