Idealized Conventional and Pressure-Assisted Thermal Preservation Processes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
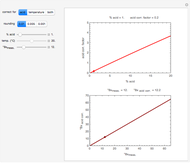
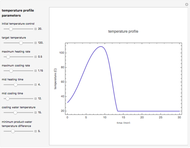
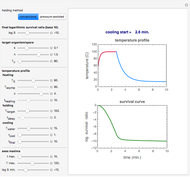
This Demonstration generates an idealized temperature profile in thermal preservation of foods or pharmaceuticals in order to reach a given survival ratio of a targeted microorganism or spore. The process can be conventional or pressure-assisted. The program calculates the time to start cooling in the former and also the holding time under pressure in the latter. It is based on the assumptions that the mortality pattern follows Weibullian kinetics, of which log-linear inactivation is a special case, and that the lethal effect during pressurization is primarily thermal.
Contributed by: Mark D. Normand, Micha Peleg, and Murray Eisenberg (April 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
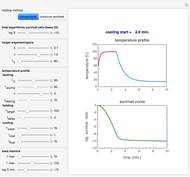
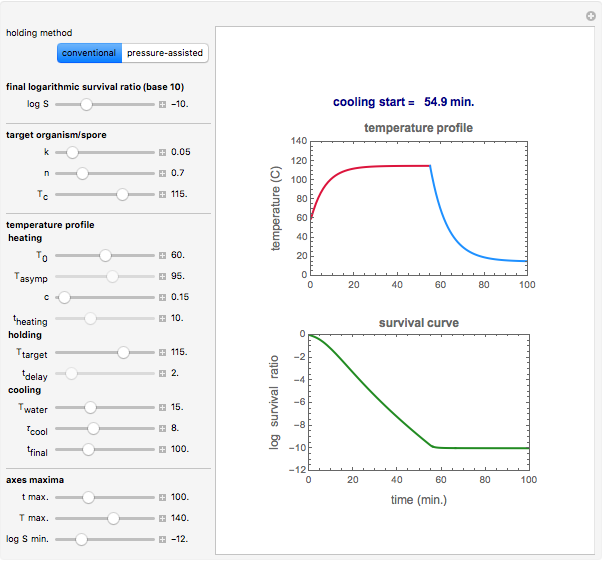
Snapshot 1: temperature profile of an idealized fast and mild conventional heat treatment and corresponding survival curve of a sensitive microorganism
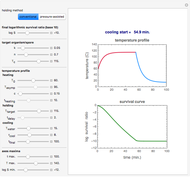
Snapshot 2: temperature profile of an idealized slow and intense conventional heat treatment and corresponding survival curve of a resistant bacterial spore
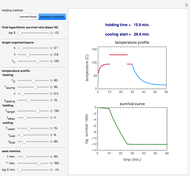
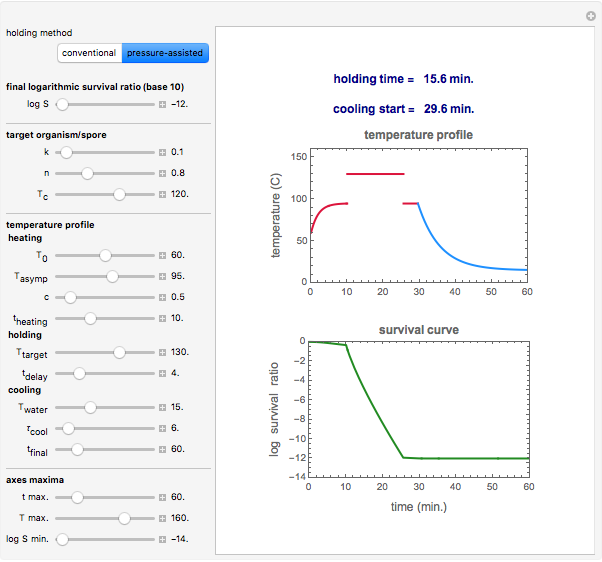
Snapshot 3: temperature profile of an idealized pressure-assisted heat treatment and corresponding survival curve of a highly heat resistant bacterial spore
Snapshot 4: temperature profile of an idealized pressure-assisted heat treatment and corresponding survival curve of a less resistant bacterial spore
Snapshot 5: temperature profile of an idealized pressure-assisted heat treatment and corresponding survival curve of a bacterial spore in a food having low thermal conductivity
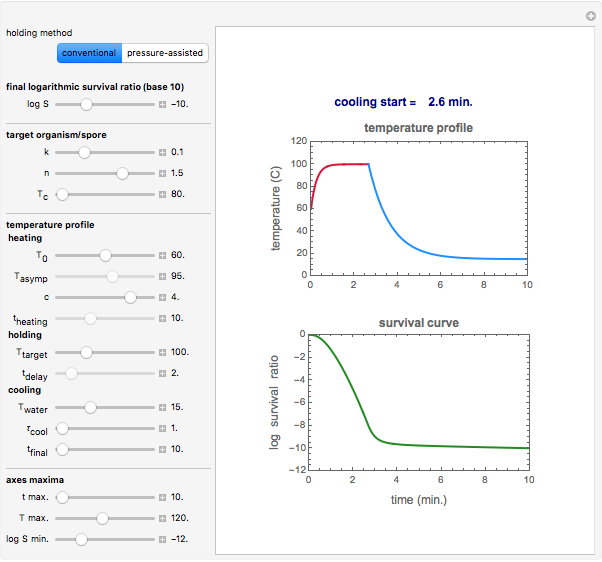
This Demonstration generates idealized temperature profiles of the kind encountered in conventional and pressure-assisted thermal preservation of food and pharmaceuticals.
The targeted organism or spore's heat resistance is specified by the WeLL (Weibullian Log Logistic) model parameters  ,
,  , and
, and 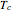 entered with sliders, where
entered with sliders, where  represents the concavity of the isothermal semi-logarithmic survival curves in the pertinent temperature range,
represents the concavity of the isothermal semi-logarithmic survival curves in the pertinent temperature range, 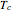 represents a marker of the beginning of the lethal temperature range, and
represents a marker of the beginning of the lethal temperature range, and  represents the slope of the Weibullian rate parameter,
represents the slope of the Weibullian rate parameter,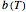 , at
, at 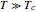 .
.
The conventional heating stage is approximated by the equation 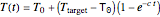 , where
, where 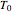 is the initial temperature,
is the initial temperature, 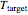 is the process temperature, and
is the process temperature, and  is a rate constant. The cooling stage is approximated by the equation
is a rate constant. The cooling stage is approximated by the equation 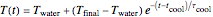 , where
, where  is the temperature of the cooling water,
is the temperature of the cooling water, 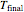 is the highest temperature reached in the process, and
is the highest temperature reached in the process, and 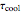 is a time characteristic of the cooling. (All temperatures are in degrees C and all times are in minutes.) The final logarithmic survival ratio,
is a time characteristic of the cooling. (All temperatures are in degrees C and all times are in minutes.) The final logarithmic survival ratio, 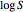 , to be accomplished by the process is entered by the user with a slider. The time,
, to be accomplished by the process is entered by the user with a slider. The time, 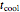 , needed to achieve this survival ratio is calculated by numerically solving the particular organism or spore's rate equation for the chosen heating and cooling curves. The numeric value of
, needed to achieve this survival ratio is calculated by numerically solving the particular organism or spore's rate equation for the chosen heating and cooling curves. The numeric value of 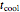 is displayed above the plots of the temperature profile and the corresponding survival curve of the process.
is displayed above the plots of the temperature profile and the corresponding survival curve of the process.
In the pressure-assisted method, chosen by clicking the "pressure-assisted" button, the conventional heating stage is approximated by the equation 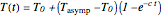 . In this process,
. In this process, 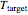 is the temperature reached almost instantaneously by adiabatic heating due to pressurization. Cooling can start immediately after depressurization or after additional holding for time
is the temperature reached almost instantaneously by adiabatic heating due to pressurization. Cooling can start immediately after depressurization or after additional holding for time 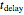 set with a slider. The cooling stage is approximated by the same equation,
set with a slider. The cooling stage is approximated by the same equation, 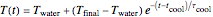 , where
, where 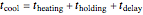 .
.
The time 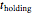 is the time at the target temperature needed to achieve the final logarithmic survival ratio,
is the time at the target temperature needed to achieve the final logarithmic survival ratio, 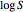 , is calculated by numerically solving the rate equation of the particular organism or spore for the chosen pressure-assisted heating and cooling regimes. The numeric values of
, is calculated by numerically solving the rate equation of the particular organism or spore for the chosen pressure-assisted heating and cooling regimes. The numeric values of 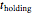 and
and 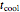 are displayed above the plots of the temperature profile and the corresponding survival curve of the pressure-assisted process.
are displayed above the plots of the temperature profile and the corresponding survival curve of the pressure-assisted process.
The generated survival curve and holding-time calculations are based on the assumptions that the inactivation pattern follows the WeLL model and that the inactivation during holding under pressure is primarily thermal. In cases where nonthermal effects of the pressure do play a significant role, comparison of the simulations with experimental results can be used to identify and quantify their contribution to the overall process lethality.
Not all possible control combinations necessarily correspond to realistic processes or can achieve the chosen final logarithmic survival ratio. If such a control combination is chosen, no curves are drawn and a message alerting the user to the situation appears in bold red text.
For more information, see Real-time generation of microbial cells' survival curves during pasteurization andReal-time generation of bacterial spores' survival curves during sterilization.
Permanent Citation