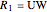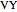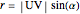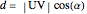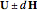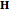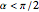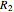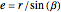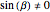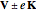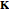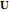Intersection of Two Lines Using Vectors

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
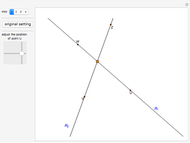
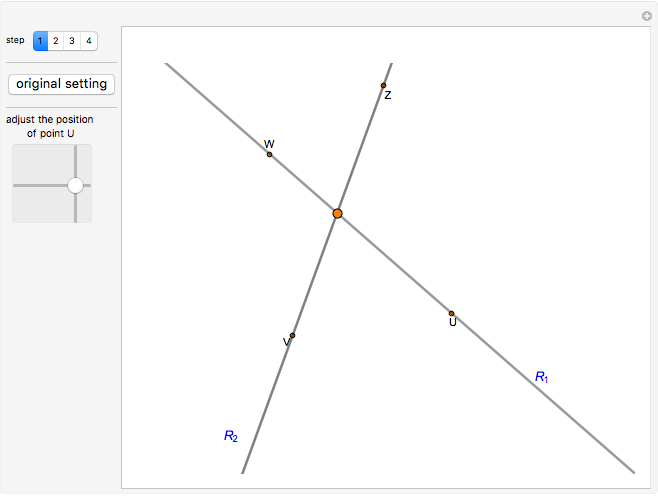
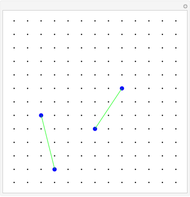
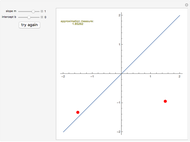
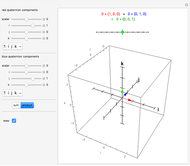
The intersection of two lines, each given by a pair of points (i.e. the respective equations are not used), is obtained by elementary vector considerations.
[more]
Contributed by: Tomas Garza (January 2012)
Open content licensed under CC BY-NC-SA
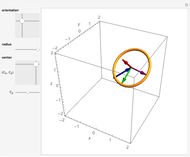
Snapshots
Details
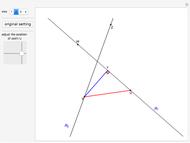
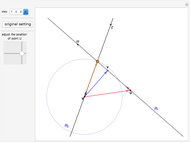
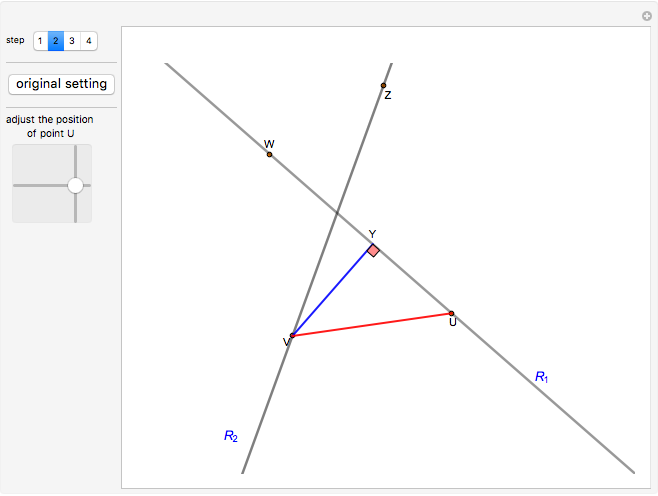
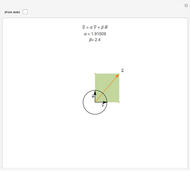
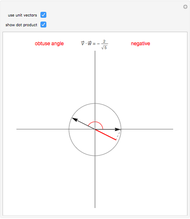
The method relies on Mathematica's capabilities to handle vectors and the angles between them. If 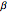 is the angle between the two lines, and
is the angle between the two lines, and  is the angle between the red segment
is the angle between the red segment 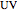 and the line
and the line 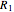 (see step 2 in the figure), then it can readily be seen that the position vector of the point of intersection is
(see step 2 in the figure), then it can readily be seen that the position vector of the point of intersection is
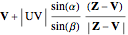 ,
,
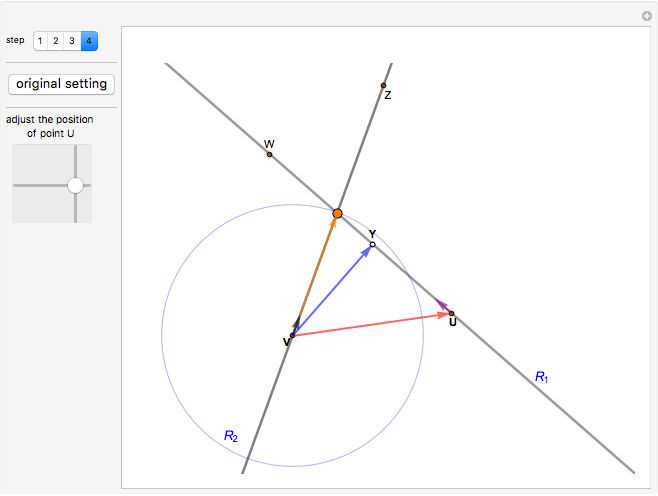
(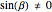 , implying that the two lines are not parallel), where
, implying that the two lines are not parallel), where 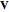 and
and 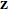 are the position vectors of the points
are the position vectors of the points 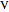 and
and  ,
, 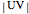 is the length of the red segment, and
is the length of the red segment, and 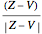 is a unit vector in the direction of the line
is a unit vector in the direction of the line 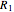 , from
, from 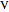 to
to  .
.
Permanent Citation