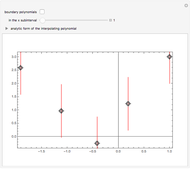
Interval Interpolating Polynomial

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
An interval interpolating polynomial is the interval function that explicitly represents the set of all real polynomials of degree  interpolating through all points from a set of
interpolating through all points from a set of  vertical segments in the plane.
vertical segments in the plane.
Contributed by: Evgenija D. Popova and Radostin Surilov (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Given a set of  distinct real numbers
distinct real numbers  and a set of
and a set of  compact intervals
compact intervals  whose end points
whose end points  are real numbers. The pair
are real numbers. The pair  is a vertical segment in the plane
is a vertical segment in the plane  Denote by
Denote by  the set of
the set of 
 vertical segments. We assume that the input data belong to the interval
vertical segments. We assume that the input data belong to the interval  , such that
, such that 
The set  of all real algebraic polynomials of degree
of all real algebraic polynomials of degree  interpolating all possible sets of points
interpolating all possible sets of points  where
where  can be represented explicitly by an interval function, called interval interpolating polynomial.
can be represented explicitly by an interval function, called interval interpolating polynomial.
The interval interpolating polynomial has the explicit representation
 (
( )=
)= ,
,
where  are the usual coefficients in the Lagrangian interpolating polynomial,
are the usual coefficients in the Lagrangian interpolating polynomial,
 .
.
At any point  the value
the value  of the interpolating polynomial is an interval.
of the interpolating polynomial is an interval.
Each vertical segment in the present Demonstration is generated as  where the point with coordinates
where the point with coordinates  is represented by a locator. Drag the locators or create/delete locators to change the vertical segments and see how the interval interpolating polynomial (in its graphical or analytical representation) changes.
is represented by a locator. Drag the locators or create/delete locators to change the vertical segments and see how the interval interpolating polynomial (in its graphical or analytical representation) changes.
The boundary of the interval interpolating polynomial consists of piece-wise real interpolating polynomials defined by particular end points of the intervals  for each subinterval
for each subinterval  Move the
Move the  subinterval slider to see the corresponding slice\[Hyphen]boundary real interpolating polynomials—one colored in orange and the other in green.
subinterval slider to see the corresponding slice\[Hyphen]boundary real interpolating polynomials—one colored in orange and the other in green.
The family of real polynomials interpolating all points in a given set of vertical segments can be investigated without using interval arithmetic [1]. Other material related to the interval interpolating polynomial, including a more general setting, can be found, for example, in [2], [4]. Another approach that is different to the interval function representation is called parameter set representation. Some material related to this approach can be found in [3].
References
[1] M. A. Crane, "A Bounding Technique for Polynomial Functions," SIAM J. Appl. Math., 29(4), 1975.
[2] J. Garloff, "Optimale Schranken bei Intervallinterpolation mit Polynomen und mit Functionen  ," Z. Angew. Math. Mech., 59, 1979 pp. T59–T60.
," Z. Angew. Math. Mech., 59, 1979 pp. T59–T60.
[3] M. Milanese, J. P. Norton, H. Piet-Lahanier, and E. Walter (eds.), Bounding Approaches to System Identification, London, N.Y.: Plenum Press, 1996.
[4] J. Rokne, "Explicit Calculation of the Lagrangian Interval Interpolating Polynomial," Computing, 9, 1972 pp. 149–157.
Permanent Citation