Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Jack Lew Signature Function

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

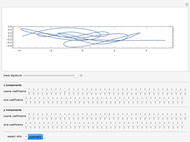
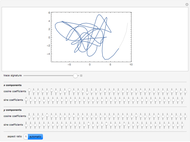
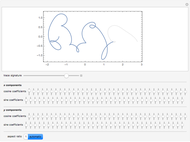
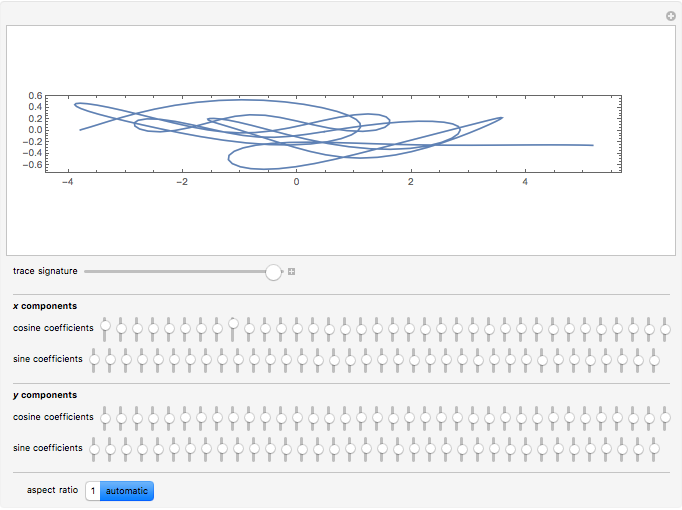
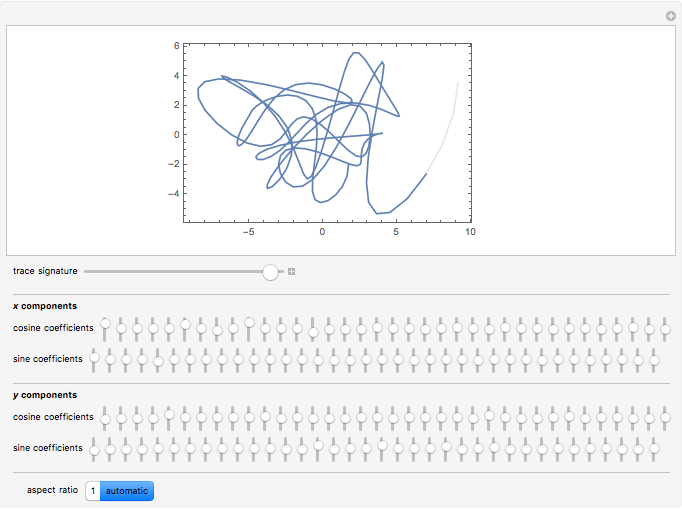
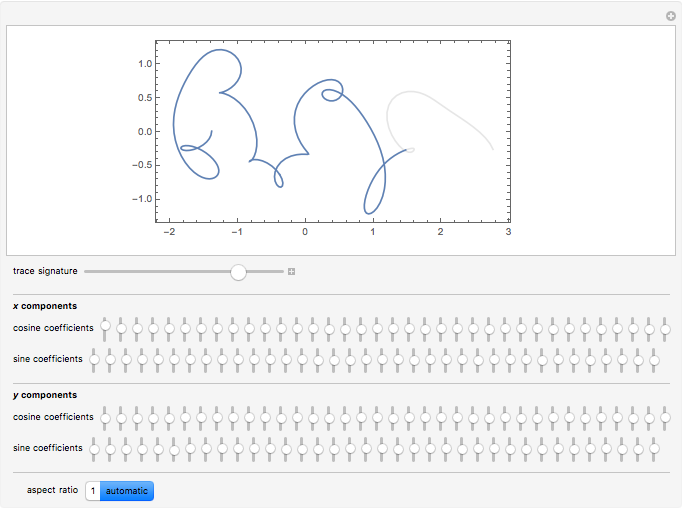
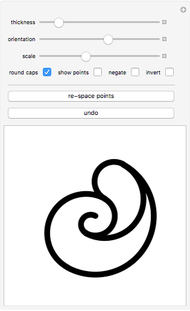
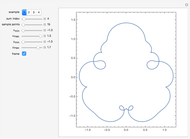
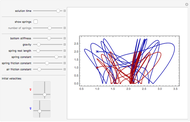
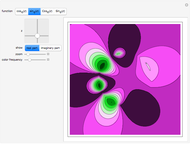
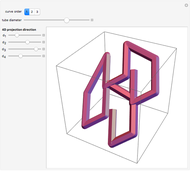
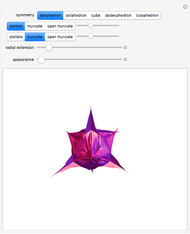
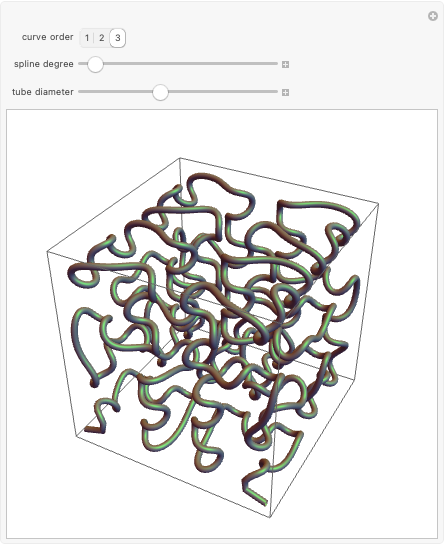
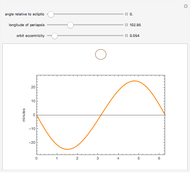
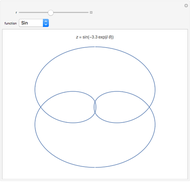
On January 9, 2013, Jack Lew was nominated to be Secretary of the Treasury. His unusual signature could soon be on all new US currency. The signature can easily be modeled with sine and cosine functions via Fourier analysis (use the initial settings).

Contributed by: Michael Trott (January 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

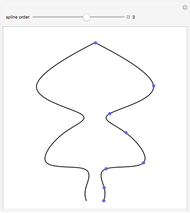
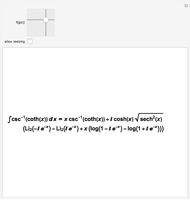
The curve has parametric equations 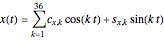; 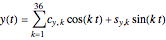. You can adjust the coefficients using the controls.

Reference

[1] C. Pierce, "Jack Lew's Signature," The Politics Blog, Esquire (Jan 10, 2013). www.esquire.com/blogs/politics/jack-lew-signature-011013.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send