Kaleidocycles

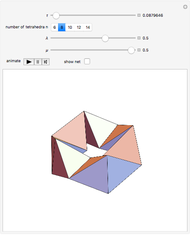
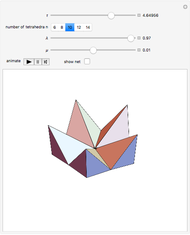
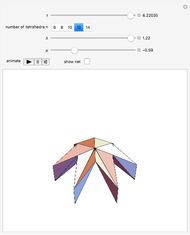
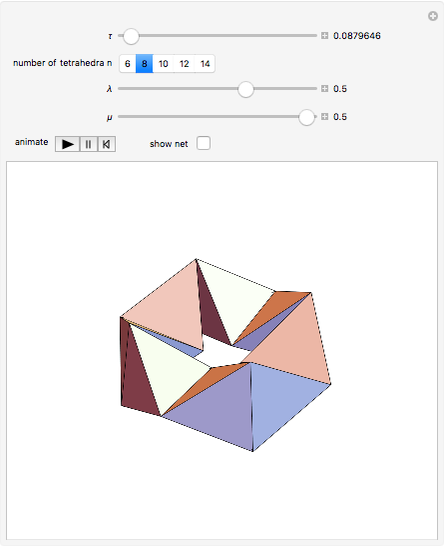
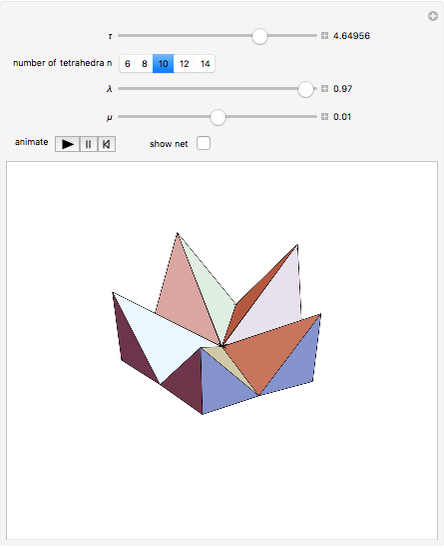
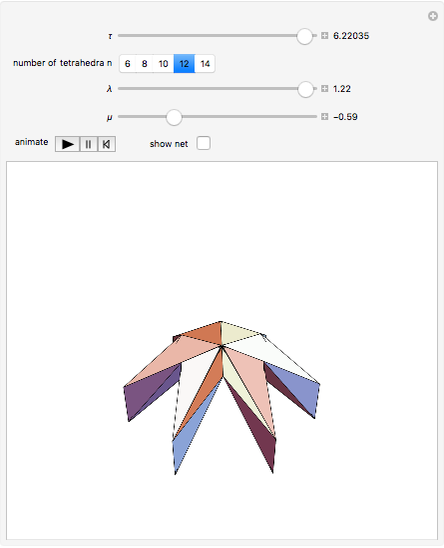
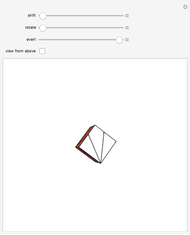
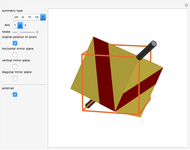
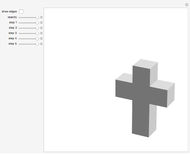
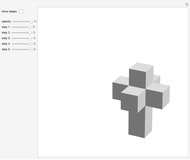
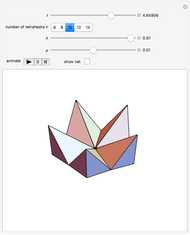
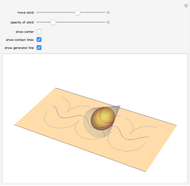
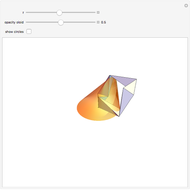
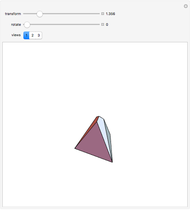
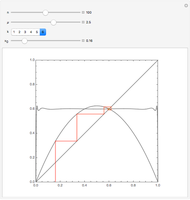
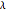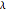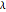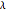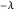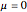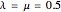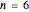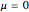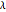A kaleidocycle is a twistable ring of tetrahedra. In the initial setting, the kaleidocycle consists of eight regular tetrahedra. You can change that number, and with the parameters 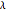and you can alter the shape of the tetrahedra.

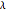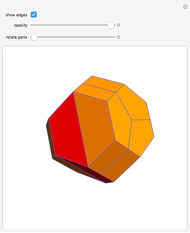
The edges with which a tetrahedron is connected to its neighbors are orthogonal. The length of one of these edges can be adjusted by the value of . When 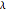is set to its maximum value, a so-called closed kaleidocycle occurs, which means that in the center the vertices of different tetrahedra touch each other at specific angles. The maximal value of 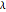depends on the number of tetrahedra. 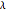The length of the other orthogonal edges is controlled by , which ranges from (in this case the faces of the tetrahedron are isosceles) to nearly 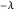(then they are lines). Other interesting values for are 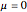, when the faces are rectangular, and 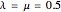, when the faces are equilateral and the tetrahedron is regular. 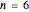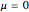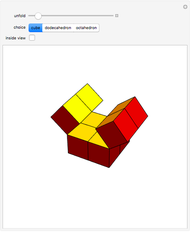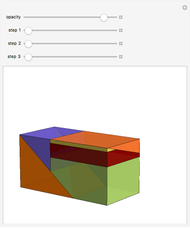For the values , , and 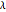set to its maximal value, the kaleidocycle becomes the middle part of the eversible cube of Paul Schatz as shown in the Demonstration "Metamorphosis of a Cube".

The inversion can be controlled with the slider or, for continuous movement, by the "animate" button. To use one of the controls, the other must be reset.