Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Life Insurance Pricing

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

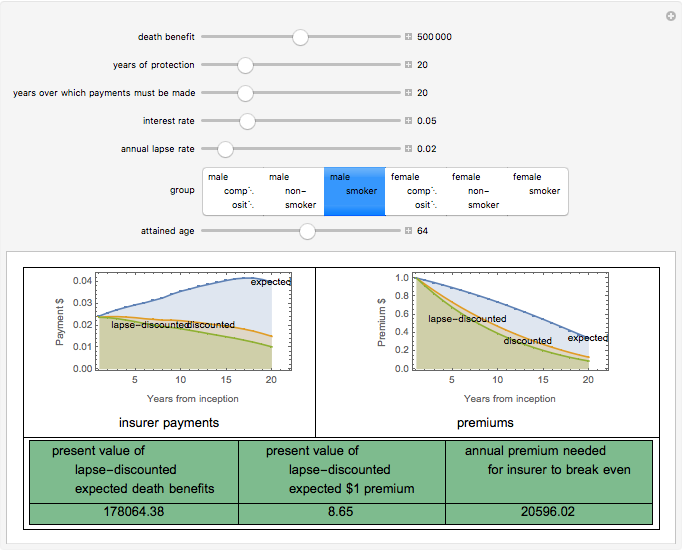
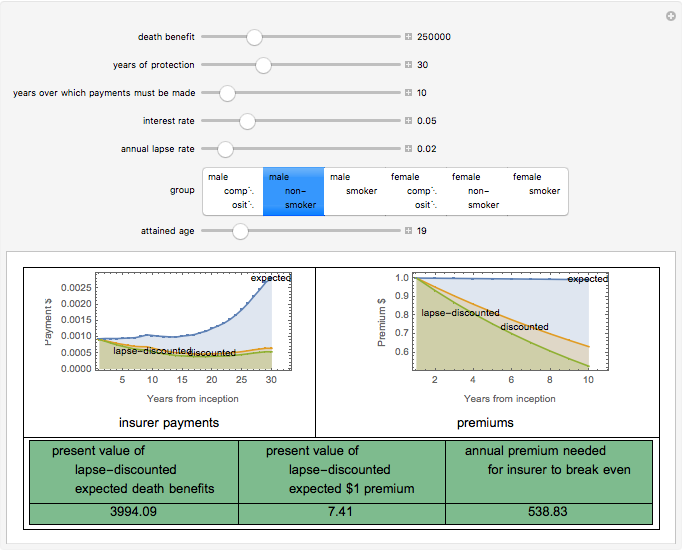
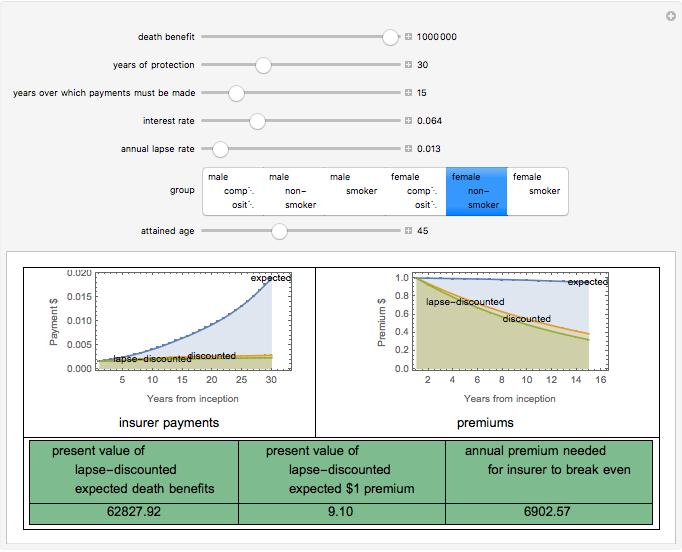
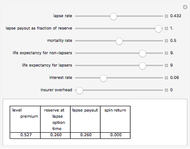
As a matter of actuarial theory, life insurance policies should be priced so that the present value of expected premiums is equal to the present value of expected death benefits. This Demonstration computes these premiums for simplified hypothetical term policies based on the 2001 CSO Mortality tables, taking into account: • the death benefit • the years of protection afforded by the policy • the years over which premiums must be paid • the interest rate the insuer expects to earn on premiums • the annual lapse rate • the gender and smoking habits of the insured • the attained age of the insured at the time of the inception of the policy.

[more]

The upper-left panel shows: • the expected payment for each year the policy is in force (blue dot) • the time-discounted expected payment (red square) • the time-discounted expected payment multiplied by the probability that the policy has not lapsed (gold diamond). The sum of the gold diamonds is equal to the present value of lapse-discounted $1 death benefits.

The top-right panel shows: • the expected premium for each year the insured must pay (blue dot) • the time-discounted expected premium (red square) • the time-discounted expected premium multiplied by the probability that the policy has not lapsed (gold diamond). The sum of the gold diamonds is equal to the present value of a lapse-discounted expected $1 premium.

The bottom panel shows the ultimate computation of the annual premium needed for the insurer to break even. Real insurance premiums will differ from this hypothetical model for many reasons, including: • overhead costs • investment rate risk (the insurer cannot know future interest rates with certainty; insurers thus guess competitively about wht returns they will actually achieve and bid for business under uncertainty about whether the rate they are offering will or will not make them a profit) • anti-forfeiture laws on certain policies • mandatory bundling of renewal options • more refined mortality models.

[less]

Contributed by: Seth J. Chandler (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The data used in this Demonstration was taken from data developed by the American Academy of Actuaries CSO Task Force from the Valuation Basic Mortality Table developed by the Society of Actuaries Individual Life Insurance Valuation Mortality Task Force, and was adopted by the National Association of Insurance Commissioners (NAIC) in December 2002. As of May 2007, it may be found online at http://www.actuary.org/life/cso/appendix_a_jun02.xls.

The model assumes that premiums are paid at the beginning of a year and deaths occur at the midpoint of the year.

If the length of time over which premiums are to be paid is longer than the term of the policy, the background turns gray, signifying that a very unusual policy has been written.

Snapshot 1: a very expensive 20-year term policy for a male smoker age 64

Snapshot 2: a 30-year term policy for a 19-year-old male non-smoker with premiums paid off at the end of the 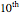year

Snapshot 3: a 45-year-old female non-smoker purchases a million dollar policy that covers her for 30 years and has premiums paid off at the end of the 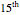year

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send