Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Magnetic Resonance and Bloch Equations

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

Many interesting cases are registered as bookmarks, which you can activate by clicking the small cross at the upper-right corner. For example:

Contributed by: Gianni Di Domenico (Université de Neuchâtel) and Antoine Weis (Université de Fribourg) (May 2008)
Open content licensed under CC BY-NC-SA

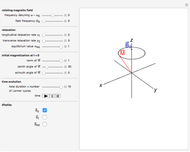
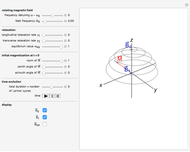
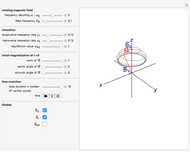
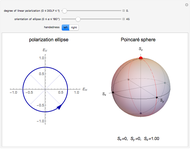
Snapshots

Details

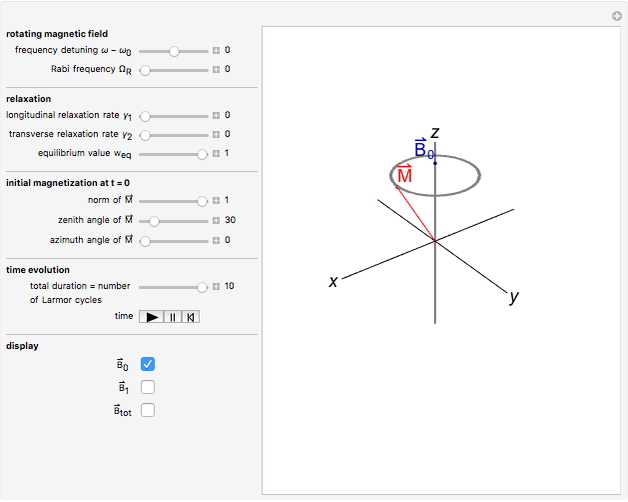
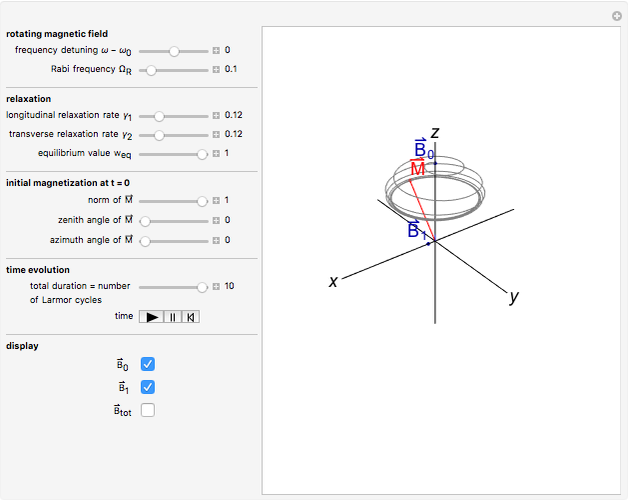
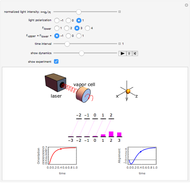
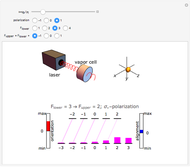
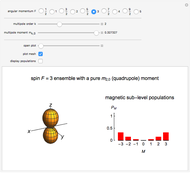
The time evolution of the magnetization 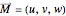of an ensemble of magnetic moments in a magnetic field 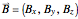is described by the Bloch equations,

Inserting 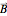into the Bloch equations yields

In the Demonstration, we set 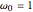, so all frequencies and relaxation rates are expressed in units of 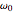. The time unit is therefore 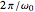and the total time is equivalent to the number of Larmor cycles.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send