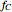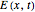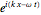Modeling a One-Cycle THz Radiation Waveform Moving through Biological Tissue

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
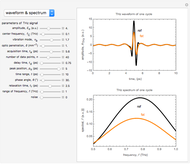
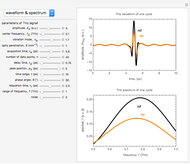
This Demonstration models a THz radiation waveform of one cycle moving through air and through biological tissue. The goal is to understand the unique characteristics of THz radiation and its interaction with biological tissue, to assist in the analysis of experiments involving radiation through a biological medium. We seek information about peak intensity, reflection, oscillations, resonant absorptions, position of surface, thickness, interface, and interface index. In the frequency domain, this central frequency of this waveform occurs at about 0.1 THz, for a bandwidth of 1 THz. These signal parameters apply for intended applications, including cancer detection. You can select parameters for THz signals in various one-cycle patterns, to tease out the dominant characteristics.
[more]
Contributed by: Muhamad Hamdi and Yusof Munajat (May 2016)
Biophysics Department, University of Riau, Indonesia
Physics Department, University of Technology Malaysia, Johor Bahru
Open content licensed under CC BY-NC-SA
Snapshots
Details
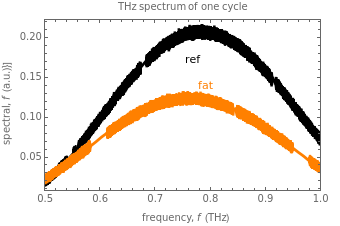
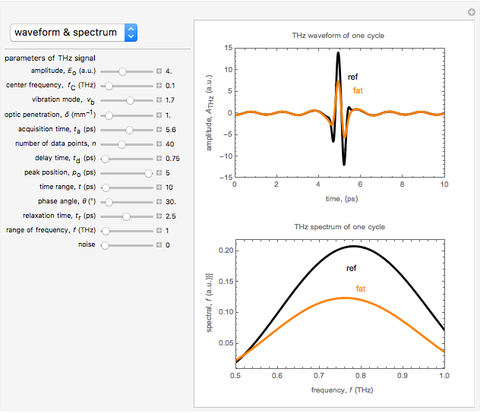
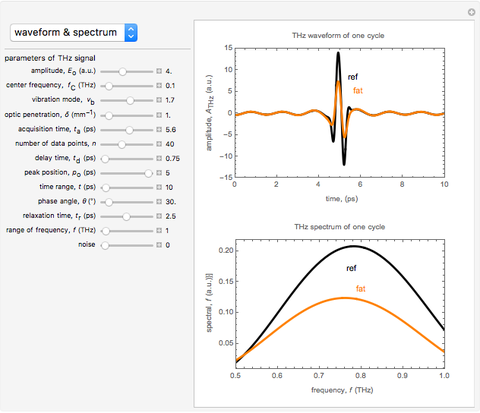
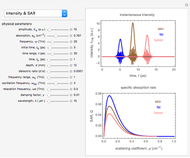
Snapshot 1: The temporal waveform shows that the signal of the THz radiation electric field depends on the time evolution, and its amplitude spectra indicates the dependence of the electric field on frequency. The amplitude spectrum extends up to 1 THz, which is partly limited by the detection response time. When the THz radiation signal propagates through various media, such as air or biological tissue, the waveform deforms gradually throughout the propagation. Air (black) and various types of tissue, such as fat (orange), show the pattern of the one-cycle THz radiation waveform. The change of signal pattern is caused by a change in parameters, with propagated medium characteristics such as absorption or attenuation coefficients, as well as dispersion phenomena.
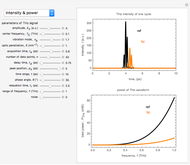
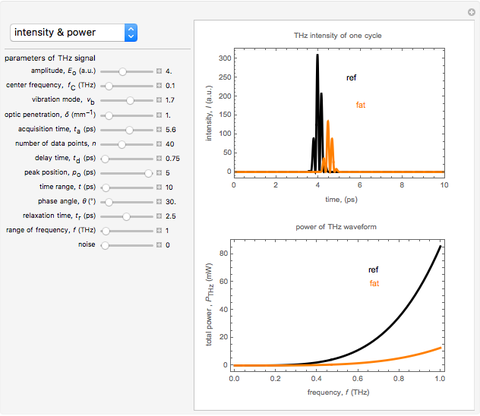
Snapshot 2: Sharp peaks in intensity indicate the magnitude of the energy flux, which is a measurement of the typical THz radiation photon flux. Meanwhile, the time-averaged THz radiation energy flux propagates radially outward with an anisotropic radiated power and angular distribution. The total radiation power increases as the square of the dipole moment and the fourth power of the frequency. The output power of a THz radiation signal emitter depends on the bias voltage and the optical pump power. The maximum radiation power is limited by the breakdown voltage of its source substrate material [1]. For air medium and various types of tissue (e.g. fat ), these show the differing reduction of intensity and power as loss of energy during absorption by the medium.
References
[1] Y.-S. Lee, Principles of Terahertz Science and Technology, New York: Springer, 2008.
[2] M. Hamdi, "Investigation on Bio-electromagnetic Field of Terahertz Radiation Behaviors at the Interface of Brain-Fat Tissue," Asian Journal of Innovation and Entrepreneurship, 1(2), 2012. journal.uii.ac.id/index.php/ajie/article/view/2826.