Motion/Pursuit Law in 1D (Visual Depth Perception 1)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
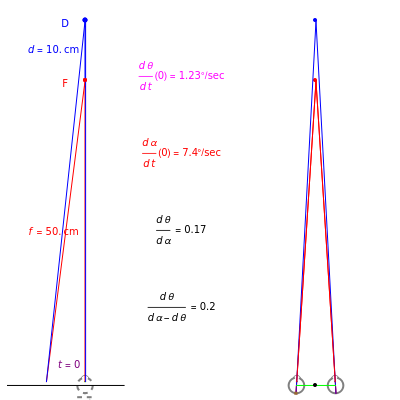
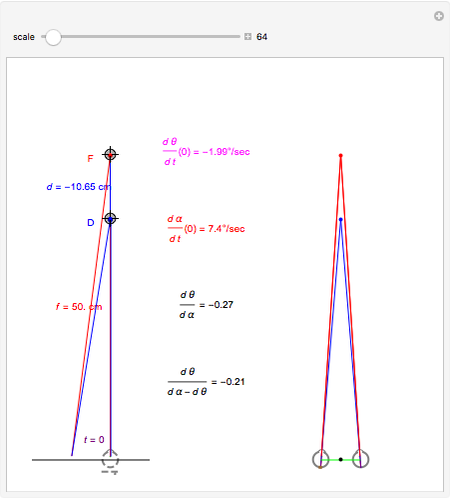
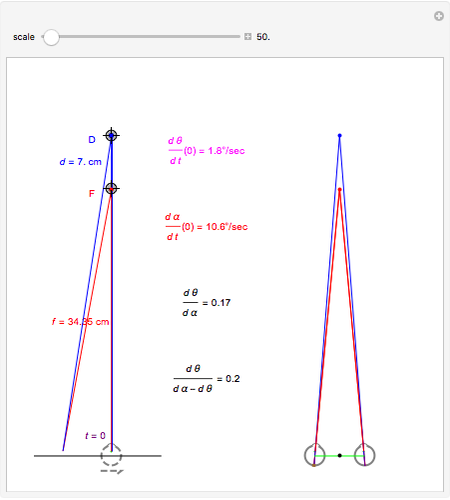
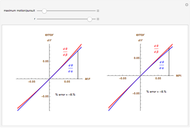
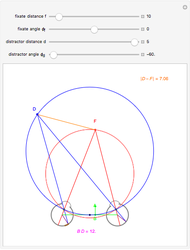
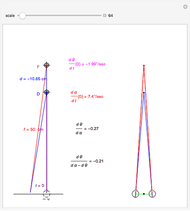
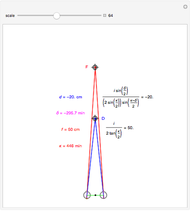
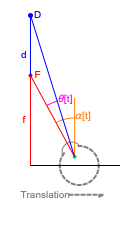
This Demonstration interactively computes retinal motion, pursuit, the motion/pursuit ratio, and the motion/pursuit law for relative depth of objects on the 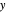 axis. The observer's eyes are "fixed" on the point
axis. The observer's eyes are "fixed" on the point 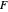 (the "fixate" point). "Fixation" means the ray from TextData["
(the "fixate" point). "Fixation" means the ray from TextData["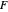 "] through the eye node strikes the fovea at the center of the retina (see: Fixation and Distraction (Visual Depth Perception 5)).
"] through the eye node strikes the fovea at the center of the retina (see: Fixation and Distraction (Visual Depth Perception 5)).
Contributed by: Keith Stroyan (September 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
We recently discovered a new formula for visual depth perception from motion parallax. Neurological work by J. W. Nadler, D. E. Angelaki, and G. C. DeAngelis in "A Neural Representation of Depth from Motion Parallax in Macaque Visual Cortex" (Nature, 452(7187), 2008 pp. 642–645) suggests that an extra-retinal signal is needed for depth perception. In the static case, retinal disparity and motor control convergence are both needed to mathematically determine depth. Our dynamic formula involves a moving retinal image cue and an eye pursuit motor control cue that we believe is the needed extra-retinal signal.
Mark Nawrot conducted psychophysical experiments that indicate people use the motion/pursuit ratio to determine depth from motion. (Our joint work has not yet appeared.) Previous work by Nawrot and others (such as M. Nawrot and L. Joyce, Vision Research, "The Pursuit Theory of Motion Parallax," 46(28), 2006 pp. 4709–4725) suggested that the motion/pursuit ratio was important. Our new formula forms a theoretical basis to understand past work, suggest new experiments, and perhaps even find a neurological basis for the formula.
Mathematica 6 played a role in this discovery and is helpful in explaining both the new dynamic formula and the old static formula for depth. There is a remarkable relation between the dynamic and static formulas. This collection of Demonstrations explains the new and old formulas interactively and lets you make your own computations. Perhaps the computations will be helpful in designing new experiments.
We begin with a description of the formula for depth from motion parallax in a symmetric case with links to Demonstrations that explain basic terms and quantities. We outline the other visual depth perception Demonstrations below.
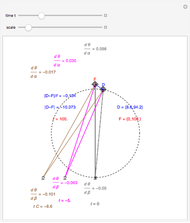
Fixation on 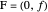 causes the eyes to rotate because of the observer's continuous translation. "Fixation" means the ray from TextData["
causes the eyes to rotate because of the observer's continuous translation. "Fixation" means the ray from TextData["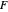 "] through the eye node strikes the fovea at the center of the retina (see: Fixation and Distraction (Visual Depth Perception 5)). Since the eye translates, it must rotate to maintain fixation (see: Tracking and Separation (Visual Depth Perception 11)).
"] through the eye node strikes the fovea at the center of the retina (see: Fixation and Distraction (Visual Depth Perception 5)). Since the eye translates, it must rotate to maintain fixation (see: Tracking and Separation (Visual Depth Perception 11)).
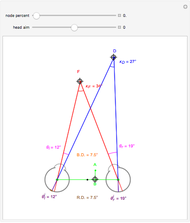
The derivative in terms of the eye parameters, the node percent 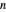 , interocular distance
, interocular distance  , and eye radius
, and eye radius  above is
above is
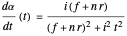 .
.
This peaks at 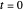 (when the denominator is largest):
(when the denominator is largest):
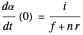 .
.
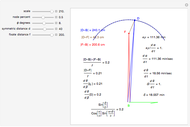
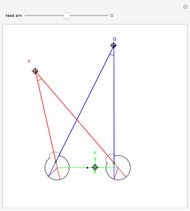
The observer's translation also causes the angle separating the fixate and distraction to change, causing motion of the image of 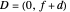 on the retina. In this case, where the distractor is also on the
on the retina. In this case, where the distractor is also on the 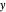 axis, at
axis, at 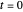 this derivative is
this derivative is
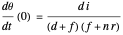 .
.
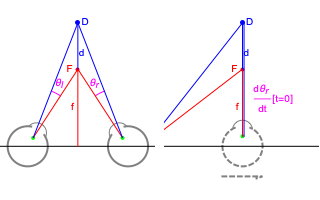
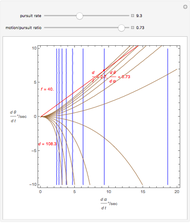
The ratio of retinal motion over pursuit is
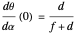 .
.
The basic case of the motion/pursuit law for relative depth from motion parallax is
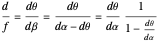
where the angle 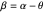 simplifies the math, but may not correspond to a neurological signal.
simplifies the math, but may not correspond to a neurological signal.
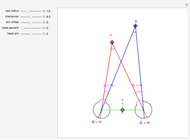
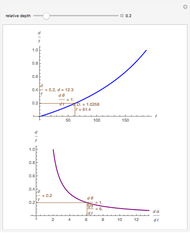
You can compute all these quantities in this Demonstration by dragging the fixate and distractor. The Demonstration "Motion, Pursuit, Fixate and Distractor (Visual Depth Perception 2)" plots the values of retinal motion and smooth eye pursuit for your choice of fixate and distractor in this basic one-dimensional setting.
The Visual Depth Perception Demonstrations
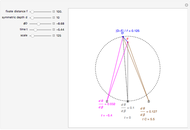
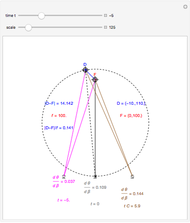
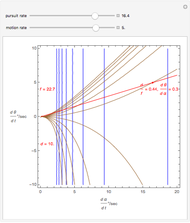
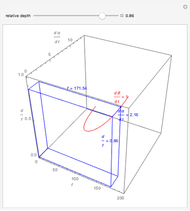
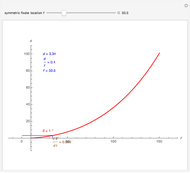
The ratio of retinal motion and tracking pursuit derivatives extends to a distractor located anywhere in the horizontal fixation plane. The Demonstrations "Motion/Pursuit Law in 2D (Visual Depth Perception 3)" and "Motion/Pursuit Law on Invariant Circles (Visual Depth Perception 4)" allow you to do computations with the 2D formula. The two-dimensional motion/pursuit law does not peak at time 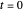 as it does in the symmetric 1D case above and the peak time value of the formula gives a good measure of the relative distance for a 2D distractor.
as it does in the symmetric 1D case above and the peak time value of the formula gives a good measure of the relative distance for a 2D distractor.
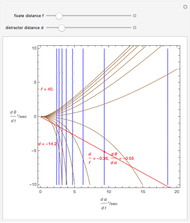
The time zero value of the motion/pursuit formula is invariant on circles with diameter on the 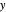 axis so it is not a good measure of relative distance when the distractor is displaced left or right. A similar thing happens with binocular disparity as explained in the Demonstration "Vieth–Müller Circles (Visual Depth Perception 8)". Binocular disparity is a well-studied static cue to depth that is explored in the Demonstrations "Binocular Disparity (Visual Depth Perception 7)" and "Disparity, Convergence and Depth (Visual Depth Perception 10)".
axis so it is not a good measure of relative distance when the distractor is displaced left or right. A similar thing happens with binocular disparity as explained in the Demonstration "Vieth–Müller Circles (Visual Depth Perception 8)". Binocular disparity is a well-studied static cue to depth that is explored in the Demonstrations "Binocular Disparity (Visual Depth Perception 7)" and "Disparity, Convergence and Depth (Visual Depth Perception 10)".
Neither binocular disparity alone nor retinal motion alone is sufficient to determine relative depth. These results are shown in the Demonstrations "Binocular Disparity versus Depth (Visual Depth Perception 9)", "Motion Parallax versus Depth, 2D (Visual Depth Perception 12)", and "Motion Parallax versus Depth, 3D (Visual Depth Perception 13)".
The remarkable connection between the new motion/pursuit formula for depth and the classical formula for depth from disparity and convergence is explored in the Demonstration "Dynamic Approximation of Static Quantities (Visual Depth Perception 14)".
We do not know a visual cue that could give a translating observer an accurate estimate of the speed of translation, but if speed is known, the motion/pursuit ratio would determine the absolute distance as you can compute in the Demonstrations "Speed, Motion, Pursuit and Depth (Visual Depth Perception 15)" and "Speed, Pursuit, M/P Ratio and Depth (Visual Depth Perception 16)".
Experimental evidence suggests that people often perceive distractors closer to them than they actually are. The motion/pursuit ratio 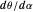 also has this property and it remains to be seen experimentally how human perception compares with
also has this property and it remains to be seen experimentally how human perception compares with 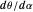 and
and 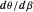 . You can explore this comparison computationally in the Demonstrations "Motion/Pursuit Ratio and Depth in 1D (Visual Depth Perception 17)" and "Motion/Pursuit Ratio and Depth in 2D (Visual Depth Perception 18)".
. You can explore this comparison computationally in the Demonstrations "Motion/Pursuit Ratio and Depth in 1D (Visual Depth Perception 17)" and "Motion/Pursuit Ratio and Depth in 2D (Visual Depth Perception 18)".
Permanent Citation