Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

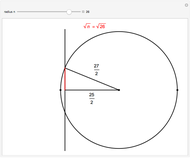
Multiwavelet Sets in the Plane

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

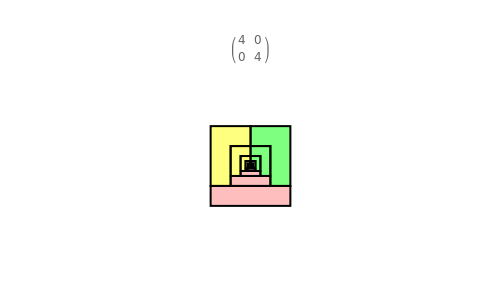
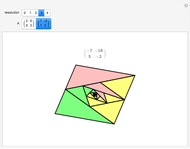
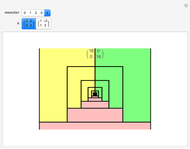
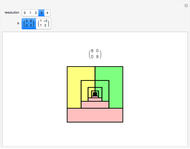
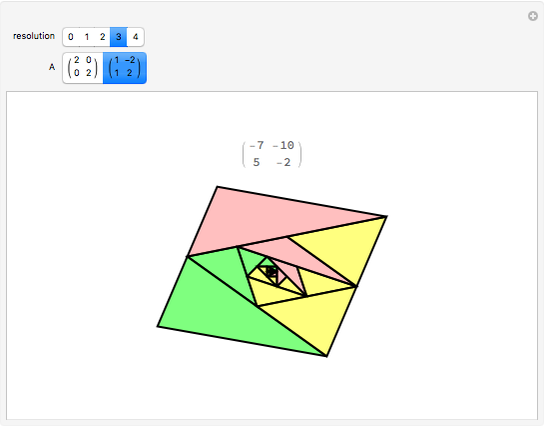
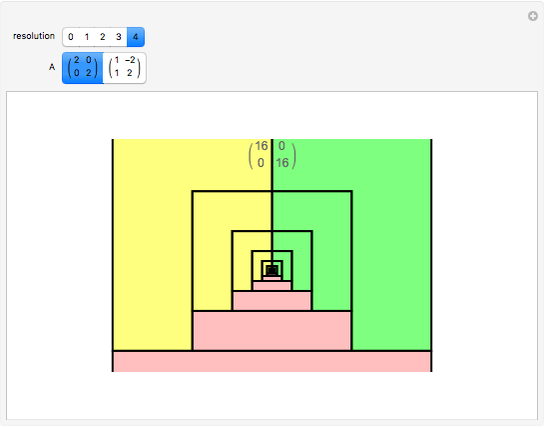
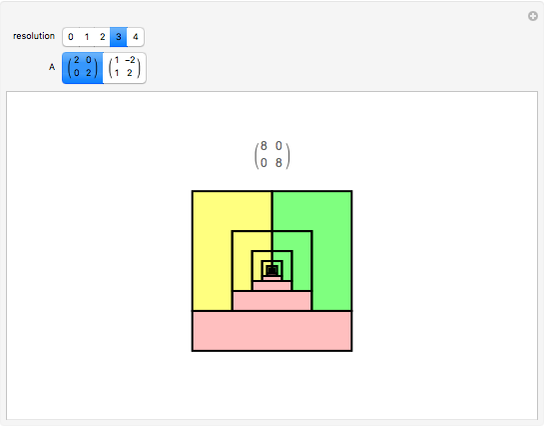
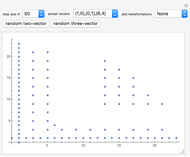
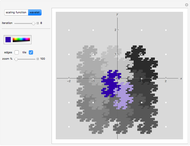
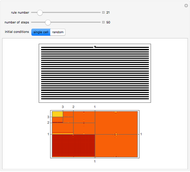
A collection of sets that can tile 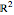by applying powers of an invertible matrix 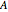are called multiwavelet sets. In this Demonstration, two examples of multiwavelet sets are given for 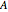equal to 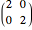or .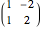

Contributed by: Vignon Oussa (January 2013)
Bridgewater State University
Open content licensed under CC BY-NC-SA

Snapshots

Details

References

[1] D. Larson, E. Schulz, D. Speegle, and K. F. Taylor, "Explicit Cross-Sections of Singly Generated Group Actions," Harmonic Analysis and Applications (C. Heil, ed.), Boston: Birkhäuser, 2006 pp. 209–230. doi:10.1007/0-8176-4504-7_ 10.

[2] X. Dai, D. Larson, and D. Speegle, "Wavelet Sets in Rn," Journal of Fourier Analysis and Applications, 3(4), 1997 pp. 451–456.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send