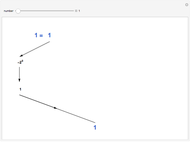
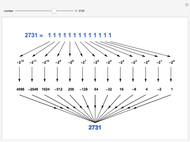
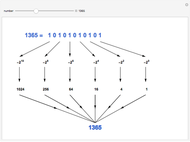
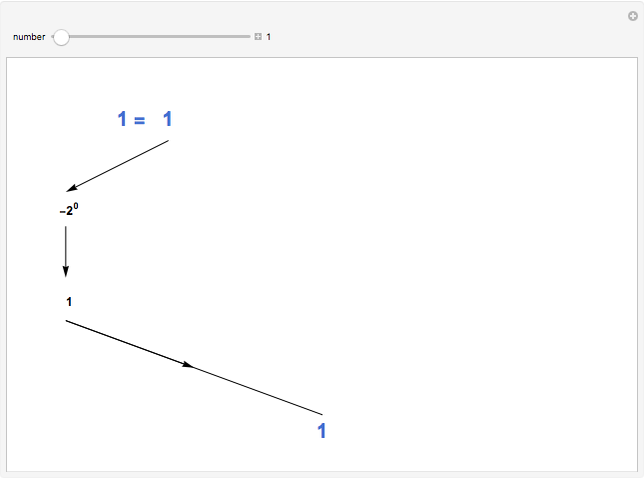
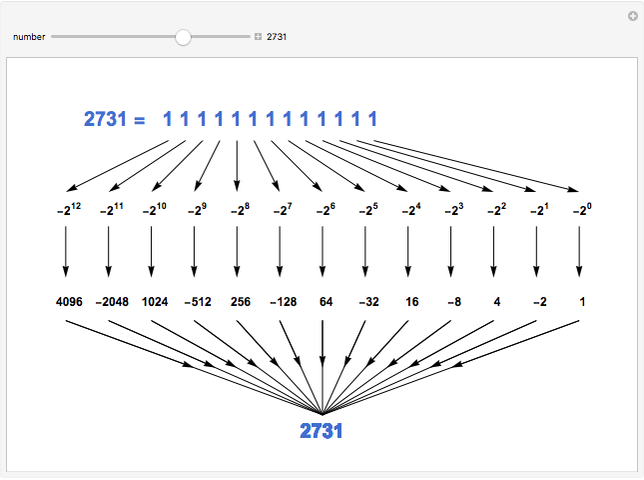
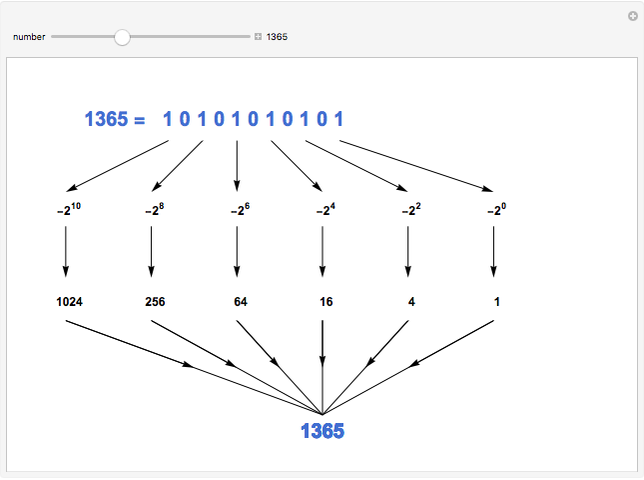
The negabinary representation of a number is its representation using base 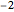. Similarly, as with the ordinary binary number base, negabinary uses the digits 0 and 1, the difference being in its use of powers of 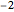to convert a negabinary number to its decimal equivalent. This Demonstration illustrates the steps of the conversion of a negabinary number into decimal. You choose a decimal number; the program converts it to negabinary and back to decimal.