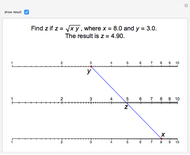
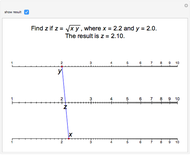
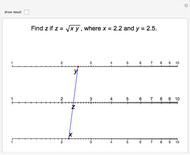
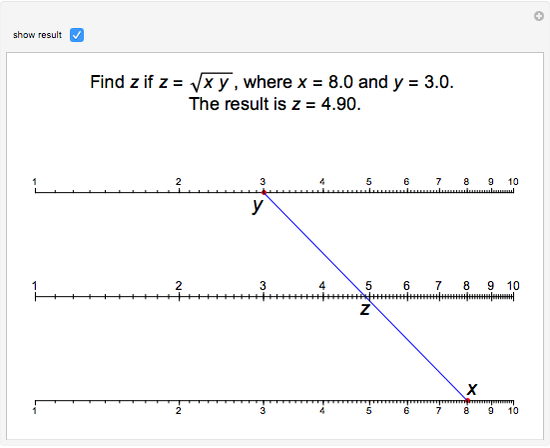
Nomogram for the Geometric Mean

Initializing live version

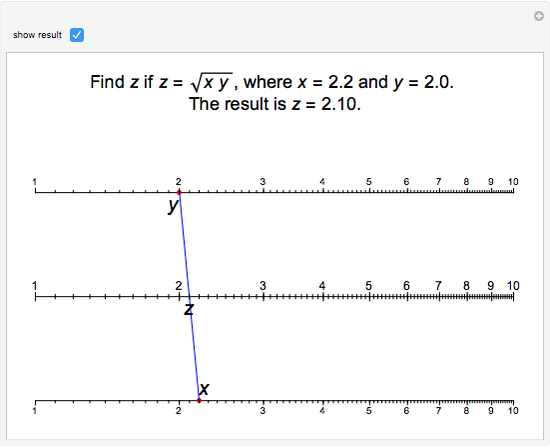
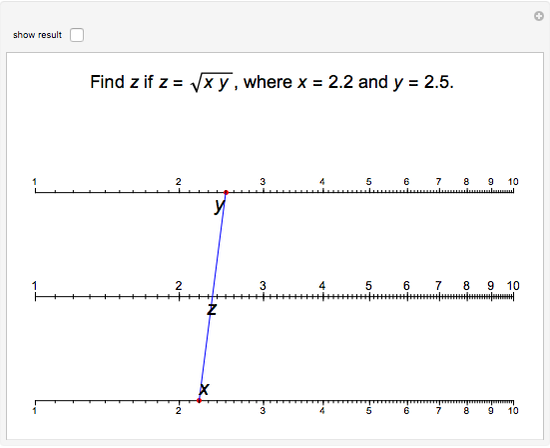
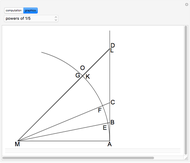
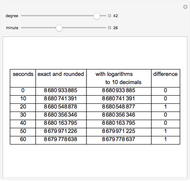
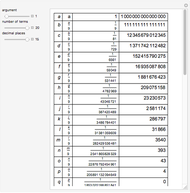
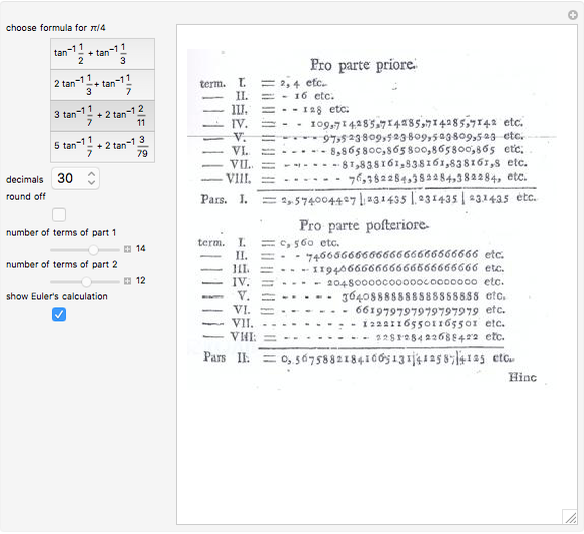
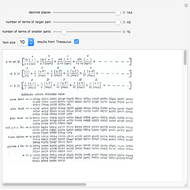
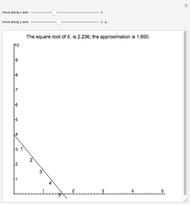
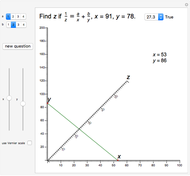
The Demonstration illustrates a nomogram to calculate the geometric mean using the identity 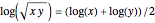. To get 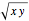, drag the red points for and .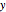

Contributed by: Izidor Hafner (September 2012)
Open content licensed under CC BY-NC-SA

Snapshots

detailSectionParagraph


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send