Details

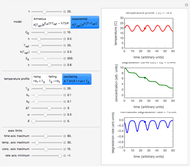
Snapshot 1: degradation curve in a reaction following the Arrhenius and first-order () kinetics equations with a linearly rising temperature

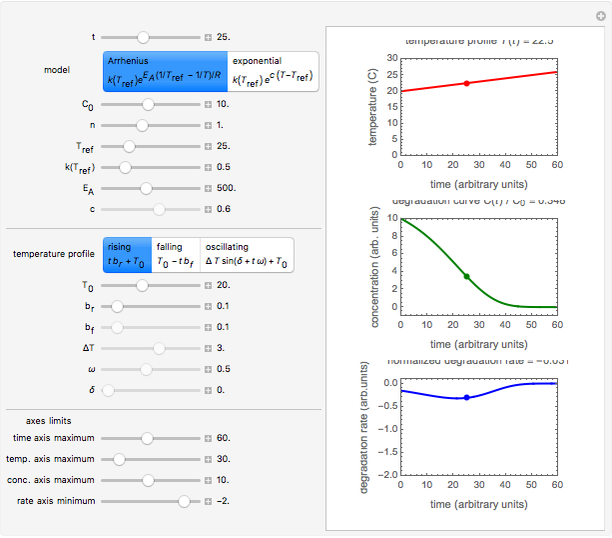
Snapshot 2: degradation curve in a reaction following the exponential model and zero-order kinetics () with a linearly falling temperature

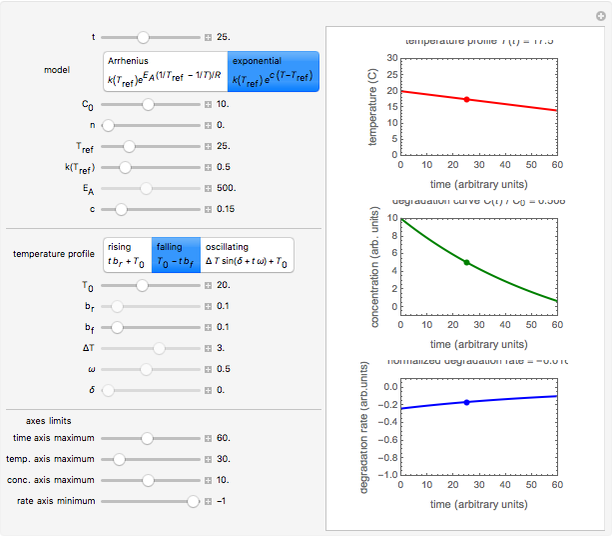
Snapshot 3: degradation curve in a reaction following the exponential model and half-order kinetics (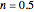) with a sinusoidally oscillating temperature

The kinetic order of a degradation reaction or decay process is defined as the exponent in the static (isothermal) rate equation 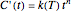with the boundary condition 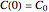in the equation representing the momentary concentration at time and the initial concentration, respectively, and 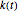, the temperature-dependent rate constant having units consistent with . When the temperature varies, 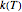becomes 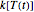and the rate equation's solution, which is more often numerical than analytical, depends on the particulars of the temperature history 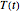. This Demonstration generates 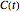curves for linearly rising, linearly falling, and oscillating (sinusoidal) temperature histories whose parameters you can enter and vary with sliders. You can also enter the order of the reaction or process in the range from 0. to 2.5 with a slider. Although the model equation for 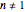applies to , we treat this scenario as a special case because of its simplicity.

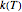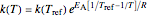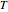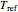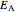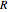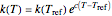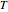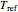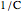The temperature dependence of the rate constant is described by either the Arrhenius equation , where and are the actual and reference temperatures, respectively, in K, is the energy of activation, and the universal gas constant, or the simpler exponential model [1] , where and are in and is a constant having units. One can show that the two models have a considerable range of overlap around the reference temperature 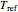and that 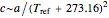or 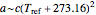, where 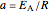[1].

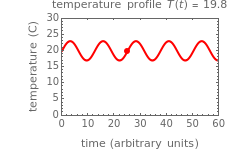
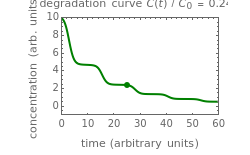
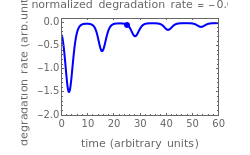
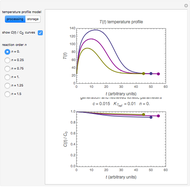
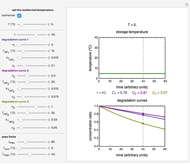
This Demonstration shows the temperature history (top) and the corresponding concentration and concentration decay rate curves (middle and bottom) with the momentary numerical values of 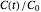and the concentration decay rate at a time (which you can choose with a slider) shown as a moving dot on the three plots.

The purpose of this Demonstration is to illustrate how a reaction's kinetic order affects the concentration decay curve under nonisothermal conditions. Therefore, not all the decay and decay rate curves that it can produce necessarily represent an actual physical disintegration or degradation process.

Reference

[1] M. Peleg, M. D. Normand, and M. G. Corradini, "The Arrhenius Equation Revisited," Critical Reviews in Foods Science and Nutrition, 52, 2012 pp. 830–851.