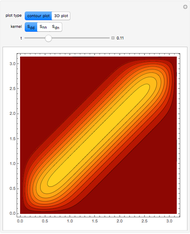
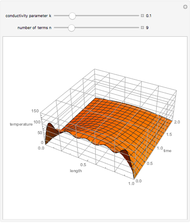
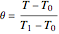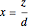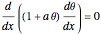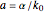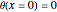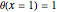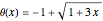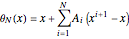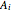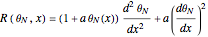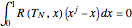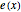One-Dimensional Heat Conduction with Temperature-Dependent Conductivity
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
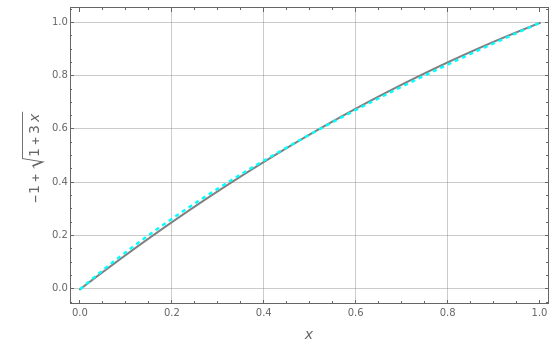
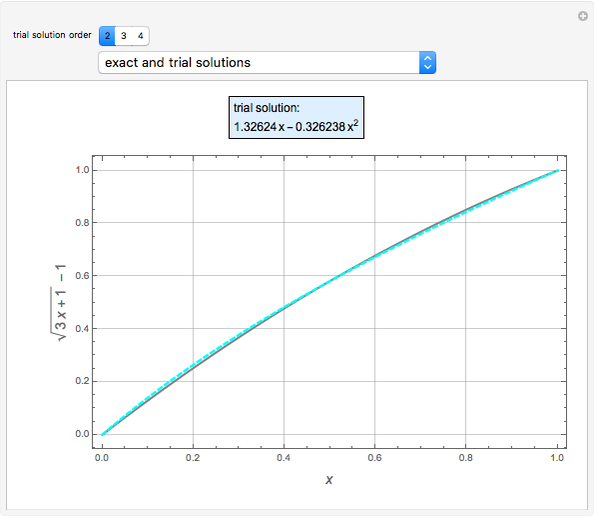
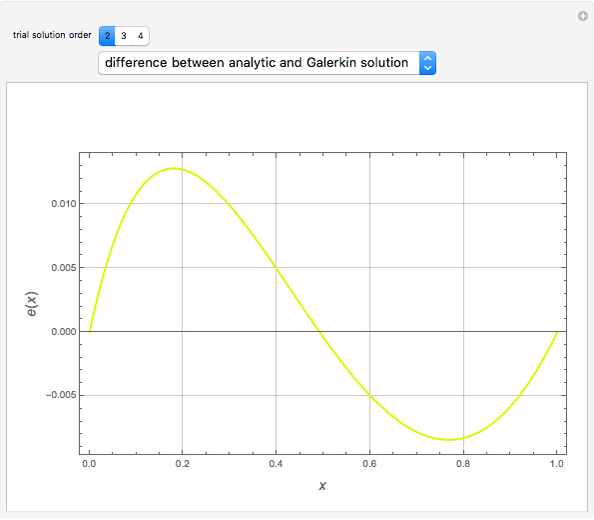
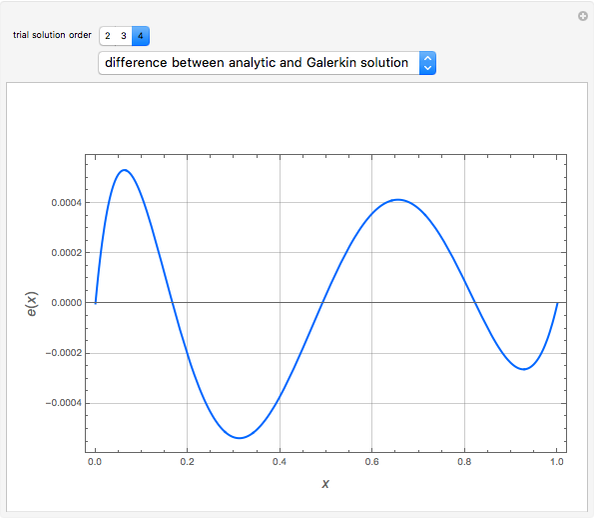
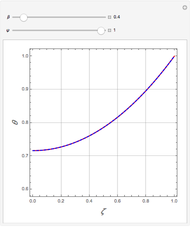
Consider the following nonlinear boundary value problem 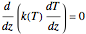 , with
, with 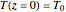 ,
, 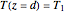 , and
, and 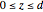 . This equation with the boundary conditions (BCs) describes the steady-state behavior of the temperature of a slab with a temperature-dependent heat conductivity given by
. This equation with the boundary conditions (BCs) describes the steady-state behavior of the temperature of a slab with a temperature-dependent heat conductivity given by 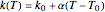 .
.
Contributed by: Housam Binous, Brian G. Higgins, and Ahmed Bellagi (April 2013)
Open content licensed under CC BY-NC-SA
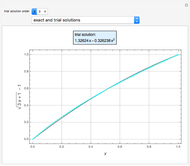
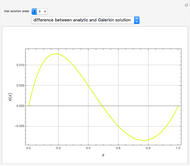
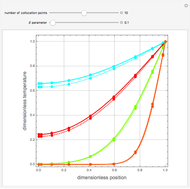
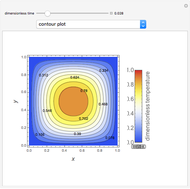
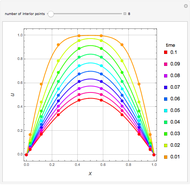
Snapshots
Details
Reference
[1] W. F. Ramirez, Computational Methods for Process Simulation, 2nd ed., Oxford: Butterworth–Heinemann, 1997.
Permanent Citation