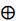Orbits of the Hopalong Map

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
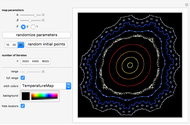
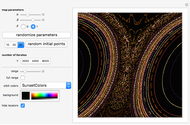
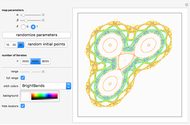
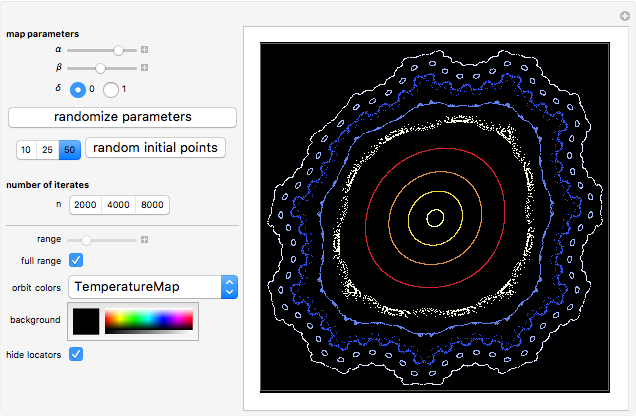
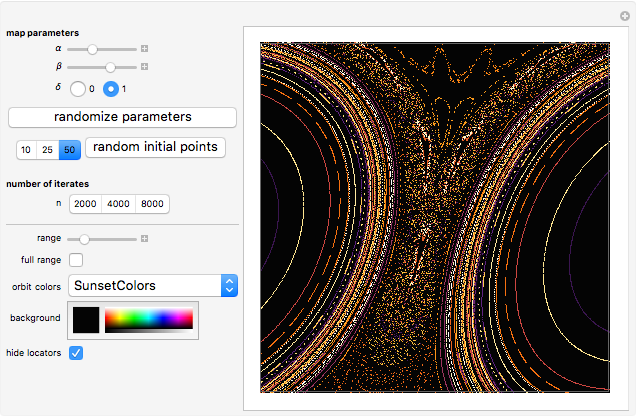
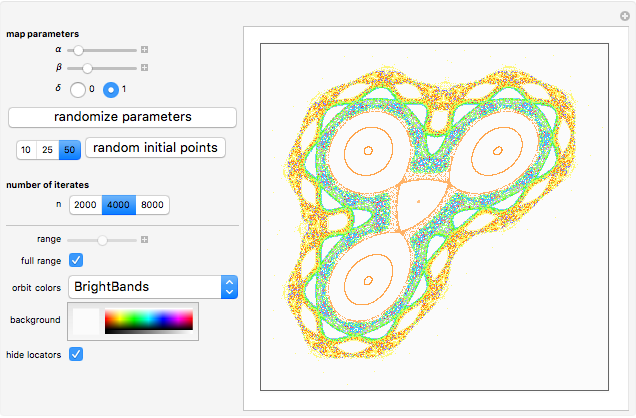
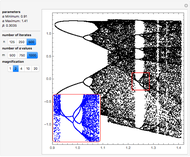
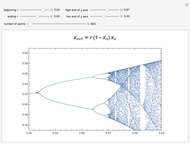
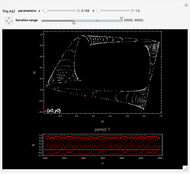
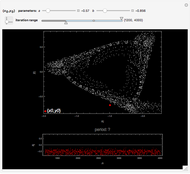
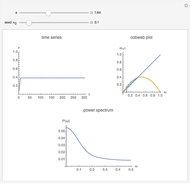
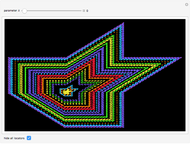
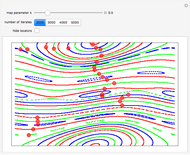
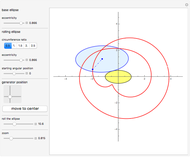
This Demonstration plots a number of orbits of the two-dimensional iterative map known as the Hopalong map. The Hopalong map can be represented by the recursion equations: 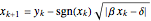 ,
, 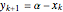 , with
, with  and
and 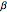 ranging over the reals and
ranging over the reals and  equal to either 0 or +1.
equal to either 0 or +1.
Contributed by: Erik Mahieu (July 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
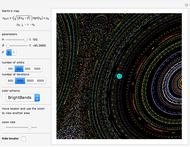
The Martin map equations were taken from [1] and [2].
The simplified, two-parameter equations for the map were suggested to the author by Barry Martin.
The Martin map is also called the "Hopalong-Attractor".
See also the German website: Huepfer.
References
[1] M. Trott, The Mathematica GuideBook for Programming, New York: Springer–Verlag, 2004 pp. 347–349.
[2] B. Martin, "Graphic Potential of Recursive Functions," in Computers in Art, Design and Animation (J. Landsdown and R. A. Earnshaw, eds.), New York: Springer–Verlag, 1989 pp. 109–129.
Permanent Citation