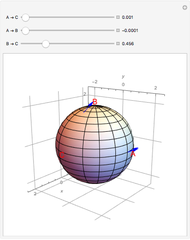
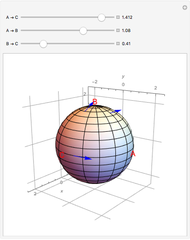
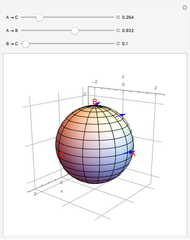
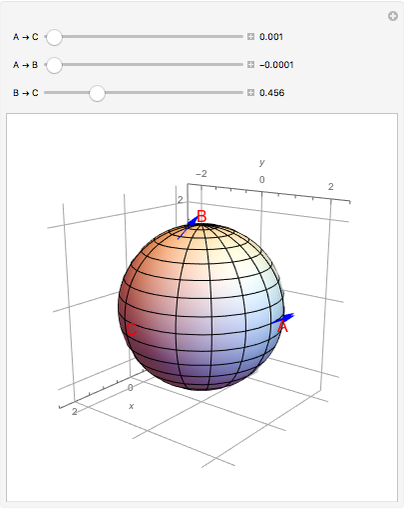
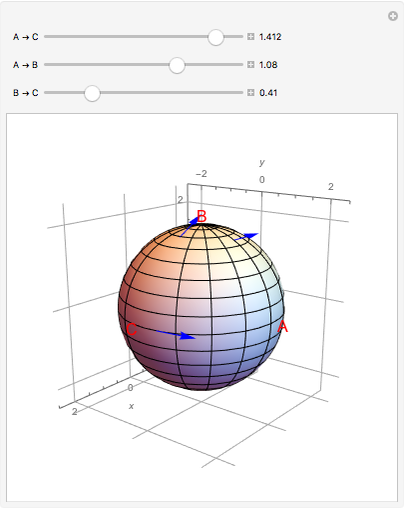
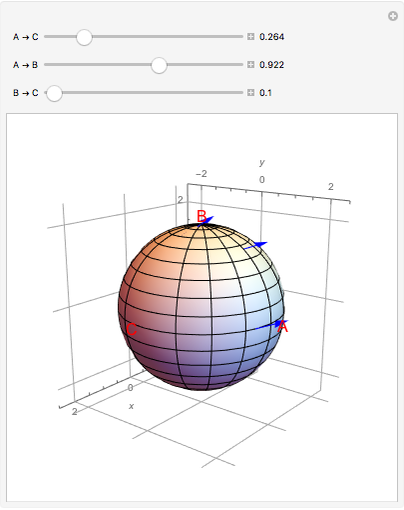
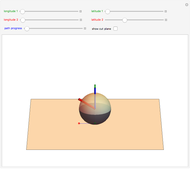
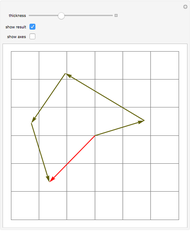
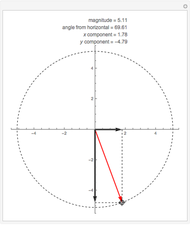
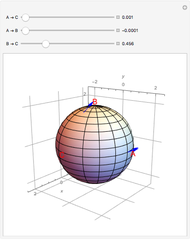
In a manifold, vector bundles can be defined as parallel [1]. This Demonstration shows how parallel transport approximately appears on a sphere (a 2-manifold). The idea behind parallel transport is that a vector can be transported about the geometric surface while remaining parallel to an affine connection, a geometrical object that connects two tangent spaces on the surface. This is shown as two vectors starting at the same point on the sphere, 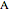; then one is transported along the geodesic (the shortest line on a surface connecting two points) from 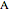to , while the other vector is shown traveling from 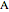to 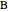, then from 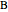to . Now the formerly parallel vectors are perpendicular, having moved on different paths on the surface, but remaining parallel to their respective connections along the way.