Polarization of Light through a Wave Plate

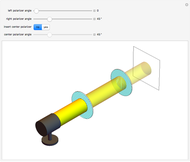
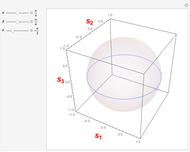
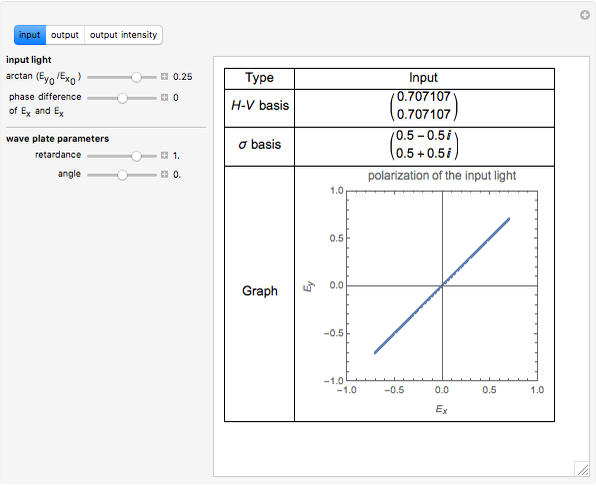
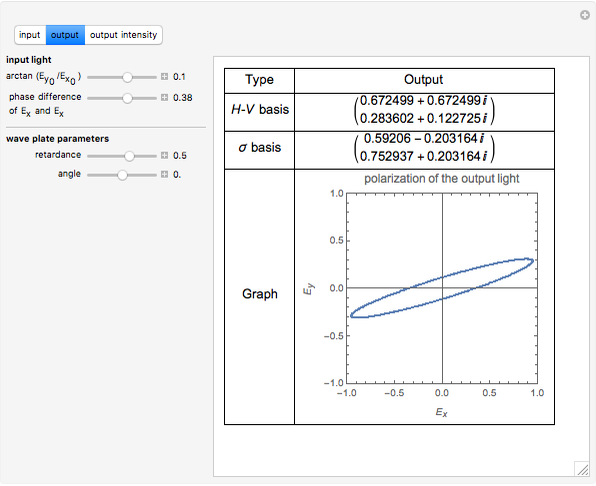
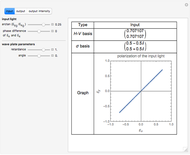
This Demonstration shows light with preferred polarization passing through a rotatable wave plate with arbitrary retardance. The light polarizations before and after passing through the wave plate are displayed.

The polarization of the input light can be decomposed into an orthogonal basis, either the 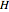- 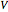basis, for horizontal and vertical linear polarization, or the basis, for right- and left-hand circular polarization. In the 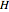- 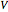basis, the input light field is decomposed into 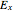and 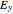components.

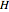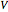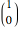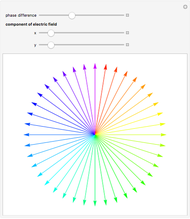
For example, horizontally polarized linear light in the - basis is , while in the basis it is 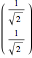. This suggests that a linear-polarized light is the equal superposition of right- and left-hand circular polarized light. The control "arctan(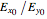)" determines the relative amplitude of the input light polarization. "Phase difference of 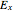and 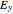" controls the phase difference between the 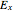and 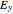fields. 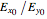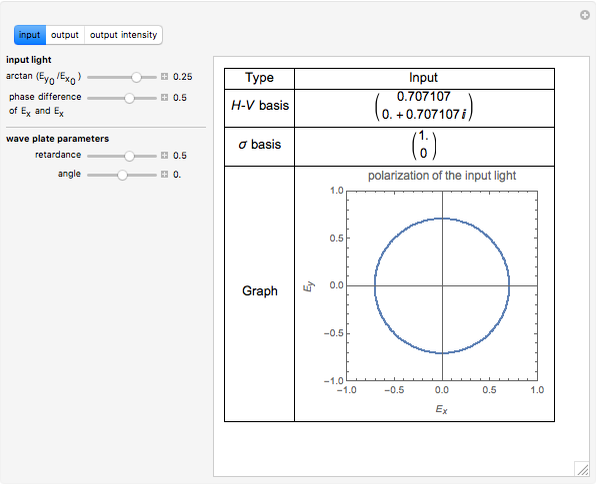For example, when both arctan() and the phase difference are set to 0, we get a horizontal linear-polarized light. When both arctan(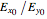) is set to 1/4 and the phase difference is set to 1/2 (in units of radians), we get a circular polarized light, with equal amplitude and a phase difference of 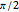between the 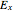and 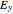fields. You can also control the retardance of the wave plate. For example, 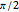radians gives a quarter-wave plate and radians gives a half-wave plate. The control "angle of wave plate" sets the optical axis of the wave plate at a given angle with respect to the axis.

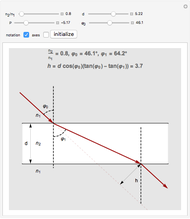
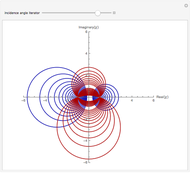
Snapshot 1: Linear-polarized light passes through a half-wave plate. The relative angle between the optical axis of the half-wave plate and the linear-polarized light is . After passing the half-wave plate, the linear-polarized light is rotated by .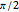

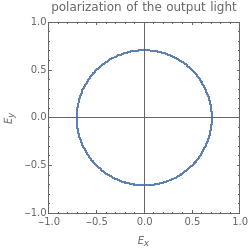
Snapshot 2: Circular-polarized light passes through a quarter-wave plate and becomes linear-polarized light.

Snapshot 3: Elliptical-polarized light passes through a quarter-wave plate.