Possible Counterexamples to the Minimal Squaring Conjecture

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
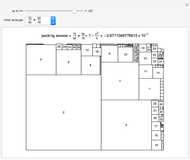
The Demonstration Minimally Squared Rectangles divides a rectangle into a minimal number of integer-sided squares. For example, a  rectangle can be divided into no fewer than 12 squares, so let
rectangle can be divided into no fewer than 12 squares, so let  . The minimal squaring conjecture implies that for any integer multiple
. The minimal squaring conjecture implies that for any integer multiple  , the same number of squares will be needed, or
, the same number of squares will be needed, or  .
.
Contributed by: Ed Pegg Jr (July 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The conjecture has been verified for all rectangles with  as shown at [2]. The method there uses Young tableaux theory, which gets very slow above size 380.
as shown at [2]. The method there uses Young tableaux theory, which gets very slow above size 380.
At [3], many squared rectangles are available that were built with the method of electrical resistance on a graph. Kirchhoff's first law is that except at a pole, the sum of the currents for any node is zero. A given graph leads to a squared rectangle, where the horizontal edges correspond to nodes and squares correspond to edges. For each horizontal edge, the sum of the squares directly over an edge squares the sum of squares directly under the edge. Perusing the squared rectangles available yielded many possible counterexamples to the minimal squaring conjecture.
The rectangles at [4] are based on planar 3-connected graphs. For 6 to 13 edges, there are 1, 0, 1, 2, 2, 4, 12, 22 such graphs ([5, A002840]). But it is possible to build rectangles from planar 2-connected graphs that have a count of 3, 7, 15, 39, 106, 316, 1026, 1643 ([5, A289471]) for 6 to 13 edges. The rectangles based on 2-connected graphs always feature two neighboring squares of the same size.
References
[1] E. Pegg Jr. "Oblongs into Minimal Squares." Mathematics Stack Exchange. (Jul 11, 2017) math.stackexchange.com/questions/2057290/oblongs-into-minimal-squares.
[2] B. Felgenhauer. "Filling Rectangles with Integer-Sided Squares." (Jul 11, 2017) int-e.eu/~bf3/squares.
[3] S. Anderson. "Squaring.Net 2016." (Jul 11, 2017) www.squaring.net.
[4] Wolfgang. "Tiling a Rectangle with the Smallest Number of Squares." MathOverflow. (Jul 11, 2017) mathoverflow.net/questions/116382/tiling-a-rectangle-with-the-smallest-number-of-squares.
[5] The OEIS Foundation. The Online Encyclopedia of Integer Sequences. A002840, A289471. oeis.org.
Permanent Citation