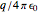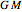Potential of a Charged Spheroid

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
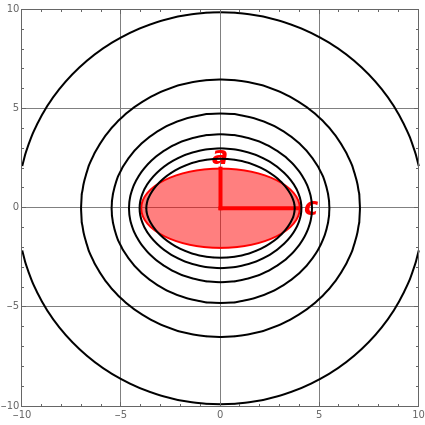
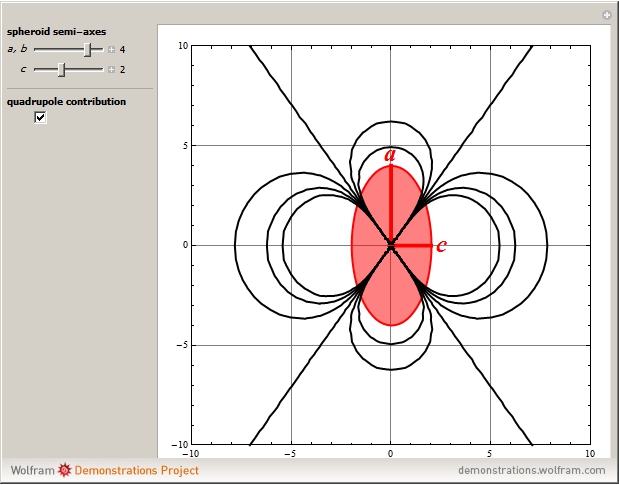
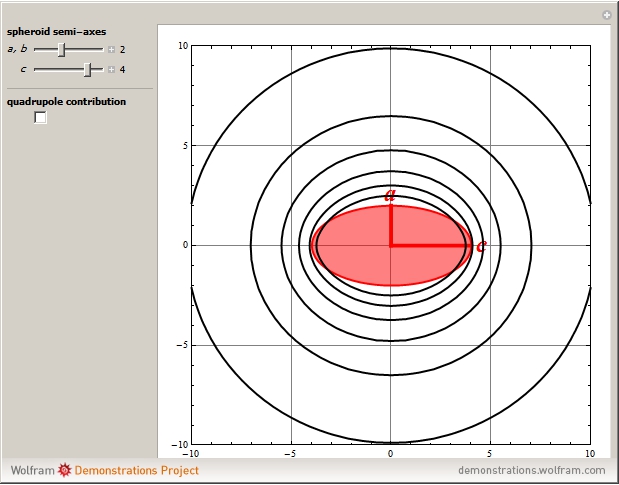
This Demonstration shows the electrostatic potential of a uniformly charged spheroid. We consider both prolate spheroids, with 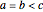 , and oblate spheroids, with
, and oblate spheroids, with 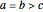 . Here
. Here  ,
,  ,
,  are the semi-axes, with the
are the semi-axes, with the  axis oriented horizontally. The potential is cylindrically symmetrical and it suffices to show just the plane containing the
axis oriented horizontally. The potential is cylindrically symmetrical and it suffices to show just the plane containing the  axis. The potential external to the spheroid is given by
axis. The potential external to the spheroid is given by 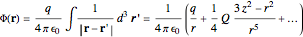 , the sum representing a multipole expansion over the charge distribution. For an oblate or prolate spheroid, the monopole contribution is dominant, with only the quadrupole term making a significant additional contribution to the potential. The quadrupole moment of a charged spheroid is given by
, the sum representing a multipole expansion over the charge distribution. For an oblate or prolate spheroid, the monopole contribution is dominant, with only the quadrupole term making a significant additional contribution to the potential. The quadrupole moment of a charged spheroid is given by 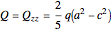 .
.
Contributed by: S. M. Blinder (August 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The potential of a spheroid with unit charge  , thus density
, thus density 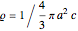 , expressed in cylindrical coordinates
, expressed in cylindrical coordinates 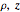 , is given by
, is given by
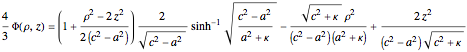 ,
,
where  is determined by the quadratic equation
is determined by the quadratic equation 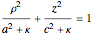 , taking the positive sign of the square root.
, taking the positive sign of the square root.
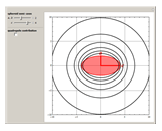
Snapshot 1: quadrupole contribution for an oblate spheroid
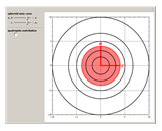
Snapshot 2: potential for a prolate spheroid
Snapshot 3: limiting case of a sphere
Permanent Citation