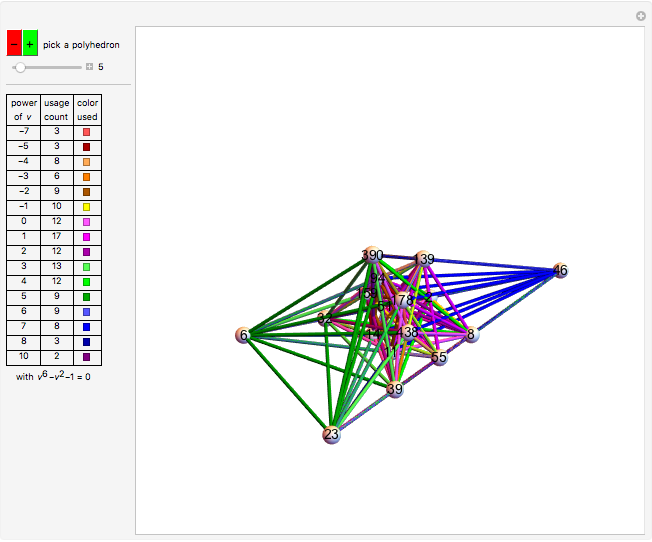
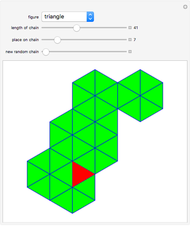
Powered Clique Polyhedra

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
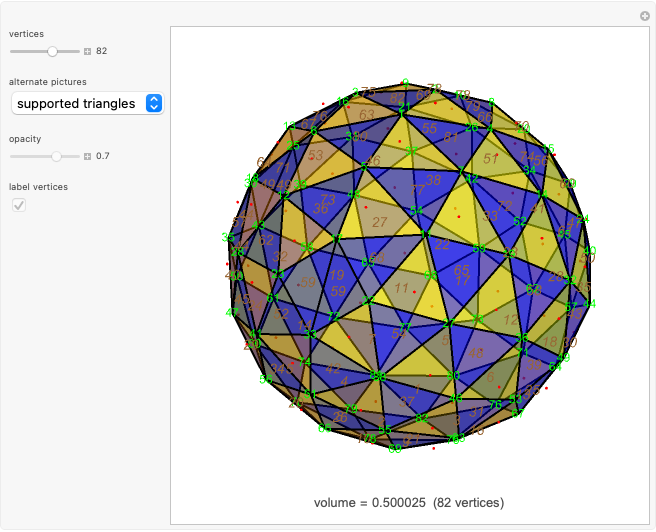
Can a tetrahedron be divided into similar tetrahedra of different sizes? The answer is not known, but a solution for triangles was found by Zak [1]. This triangle, shown further in [2], has edges that are all powers of 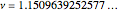 , a root of
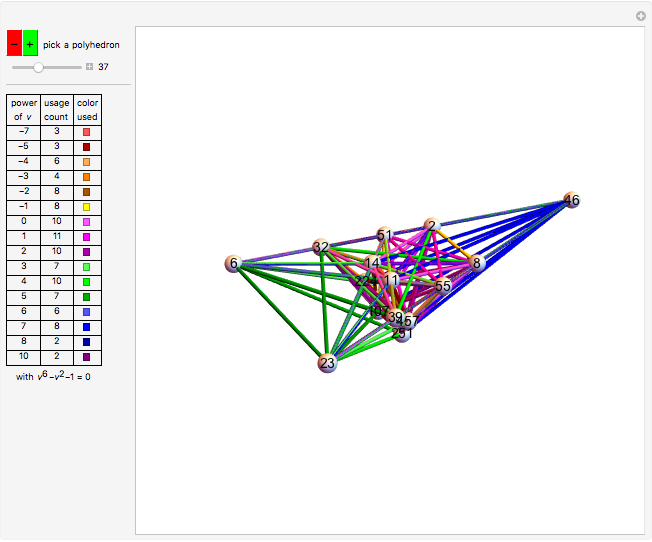
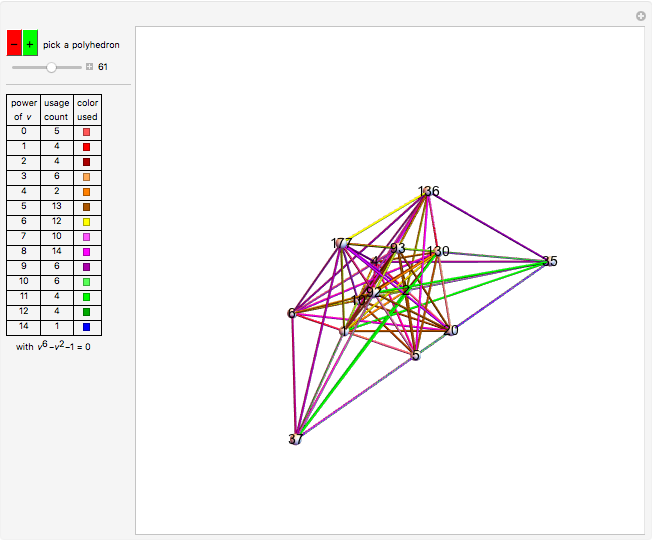
, a root of 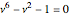 . In my Demonstration [3], I showed other polygons that could be wheel-divided into similar powered triangles. These wheels used many polynomials, but
. In my Demonstration [3], I showed other polygons that could be wheel-divided into similar powered triangles. These wheels used many polynomials, but 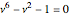 was special among them, occurring more than three times as many times as any other in the set of solution polygons.
was special among them, occurring more than three times as many times as any other in the set of solution polygons.
Contributed by: Ed Pegg Jr (July 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] A. Zak, "A Note on Perfect Dissections of an Equilateral Triangle," Australasian Journal of Combinatorics, 44, 2009 pp. 87–93. ajc.maths.uq.edu.au/pdf/44/ajc_v44_p087.pdf.
[2] E. Pegg Jr. "Zak's Triangle" from Wolfram Community—A Wolfram Web Resource. community.wolfram.com/groups/-/m/t/851275.
[3] E. Pegg Jr. "Wheels of Powered Triangles" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/WheelsOfPoweredTriangles.
Permanent Citation