Principal Stresses and Mohr's Circle for Plane Stress

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
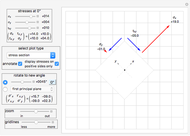
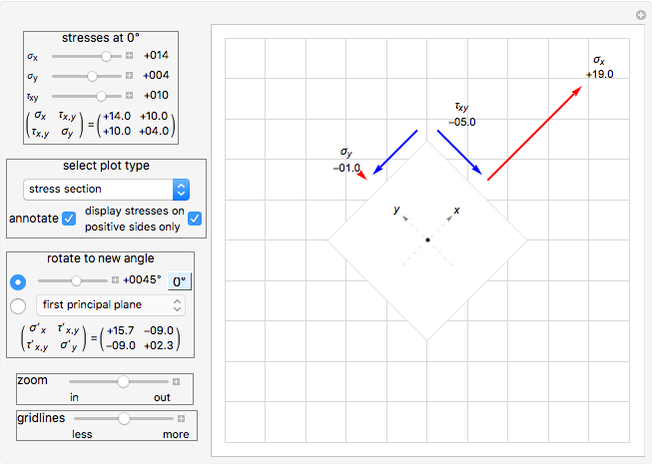
This Demonstration generates Mohr's circle for plain stress. The input is stress values for 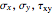 at the
at the  and
and 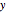 orthogonal positive faces oriented at zero angle. The Demonstration calculates Mohr's circle and generates other plots to illustrate how stress changes at different orientations as the angle of the plane is changed. Planar stress is assumed, therefore stresses in the
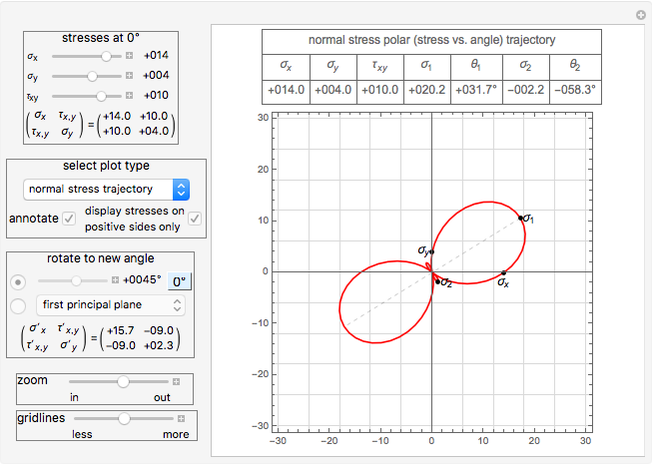
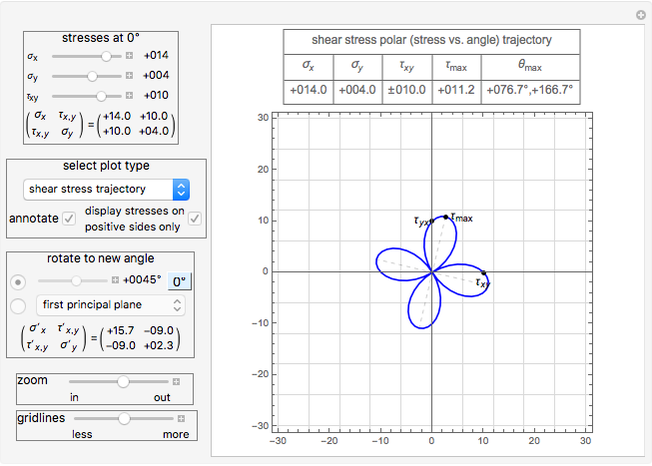
orthogonal positive faces oriented at zero angle. The Demonstration calculates Mohr's circle and generates other plots to illustrate how stress changes at different orientations as the angle of the plane is changed. Planar stress is assumed, therefore stresses in the  direction are assumed to be zero. The principal stresses (value of maximum normal and shear stresses found as the plane is rotated) are shown as red dots on the circle. The current value of the normal and shear stresses on the positive and opposite side of the plane are also shown at the end of the dashed red line (the first value is the normal stress and the second value is the shear stress). These are updated as you rotate the plane. The black dots on the edge of the circle are the locations of the stresses at zero degree and these do not move as the plane is rotated.
direction are assumed to be zero. The principal stresses (value of maximum normal and shear stresses found as the plane is rotated) are shown as red dots on the circle. The current value of the normal and shear stresses on the positive and opposite side of the plane are also shown at the end of the dashed red line (the first value is the normal stress and the second value is the shear stress). These are updated as you rotate the plane. The black dots on the edge of the circle are the locations of the stresses at zero degree and these do not move as the plane is rotated.
Contributed by: Nasser M. Abbasi (December 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In plane stress, components 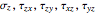 vanish and the 3D stress tensor
vanish and the 3D stress tensor 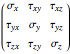 reduces to
reduces to 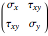 . Assuming
. Assuming 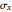 ,
, 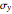 , and
, and 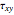 are given at 0°, the stresses
are given at 0°, the stresses 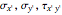 at a different angle θ are found from
at a different angle θ are found from 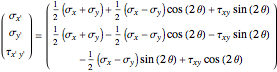 .
.
The angles 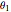 and
and 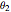 at which the maximum and minimum normal principal stress
at which the maximum and minimum normal principal stress 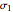 occurs are given by
occurs are given by 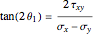 and
and 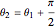 , respectively. The maximum and minimum normal principal stresses are given by
, respectively. The maximum and minimum normal principal stresses are given by 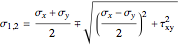 , where
, where 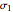 is taken as the larger of the two principal stresses in absolute terms. The maximum shear stress is at
is taken as the larger of the two principal stresses in absolute terms. The maximum shear stress is at 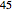 ° from the principal plane and is given by
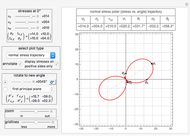
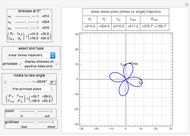
° from the principal plane and is given by 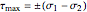 . At the principal planes the shear stress is always zero. Mohr's circle for plain stress can be viewed from the pulldown menu. You can view polar plots that show how the normal and shear stress change with angle. You can select the angle to view the stresses by using the slider or select specific planes using the pulldown menu. All units are assumed to be in SI.
. At the principal planes the shear stress is always zero. Mohr's circle for plain stress can be viewed from the pulldown menu. You can view polar plots that show how the normal and shear stress change with angle. You can select the angle to view the stresses by using the slider or select specific planes using the pulldown menu. All units are assumed to be in SI.
References
[1] A. C. Ugural, S. K. Fenster, Advanced Strength and Applied Elasticity, New York: Elsevier, 1987.
[2] REA's Problem Solver's Strength of Materials & Mechanics of Solids, New Jersey: Research and Education Association, 1996.
[3] Irving H. Shames, Mechanics of Deformable Solids, Prentice-Hall, Inc. N.J. 1964.
Permanent Citation